Performance engineering

Why are CUDA kernels hard to optimize?

Posted on by Wayne Joubert

Explosive datacenter demand has caused developers to leave no stone unturned in search of higher efficiencies. The DeepSeek team, not satisfied with Nvidia’s CUDA libraries, used a virtualized form of assembly language (PTX) to write kernel codes to accelerate their AI computations. Others have attempted to generate optimized kernels using AI, though some results have been questioned (for various attempts, see also here, here, here, here and here).

Why is it hard to write peak-speed GPU code? Writing really fast code has always been arduous, but it seems especially so for modern GPUs.

To understand the issues, my colleagues and I performed a detailed study of GPU kernel performance, across eight different GPU models from three GPU vendors [1]. The test case we considered was low precision matrix multiply, a resource-intensive operation for LLM training. We ran many, many experiments to understand what causes performance variability and why kernels sometimes run slower than you’d think they should.

For the cases we studied, we found about half a dozen different factors, but the upshot is this: modern processors like GPUs have become so complex—notably their multi-layered hierarchical memory subsystems—that it is difficult to get consistently high performance across all problem sizes a user might want to run in practice. As a result, the performance for the target problem might be surprisingly and mysteriously less than the advertised peak performance for the operation in question. The reasons might be obvious—like cache line misalignment—or more opaque. For the matrix multiply case, various issues like the need for prefetching, caching, tiling and block size selection, make it difficult for the kernel developer to optimize for every input size a user might specify.

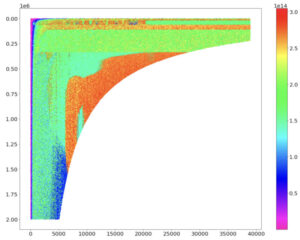
Below is an example graphic from our paper. The color indicates floating point operation rate (FLOPs) for a reduced precision matrix multiply on a representative GPU using a library call. The horizontal and vertical axes refer to the matrix dimensions for the problem (see paper for details). Though some regions show performance near the theoretical peak (red), other immediately adjacent regions show problem sizes that run dramatically less—in fact, only about half of peak performance, or less. Presumably this is because either individual kernel performance or the selection of kernels used by the library is suboptimal. The net outcome is, if your problem lands a “bad” region, you’re in for a big surprise, your performance will be much less than expected, and you may not understand why. All high-performing GPUs we tested showed irregular behaviors such as this [2] [3].

In the past this was not always a problem.  Older architectures like Sun Sparc or Cray vector processor, complex as they were, were simple enough that a reasonably well-tuned computational kernel might run well across most if not all inputs [4]. Today, performance is much harder to predict and can vary substantially based on the requested problem sizes.

This is a tough challenge for library developers. Whenever a new GPU model family comes out, new kernel optimization and tuning are required to give (hopefully) more consistently high performance, and some cases get more developer attention than others due to customer needs and limited developer resources. As a result, infrequently used operations do not get as much attention, but they may be the exact ones you need for your particular case [5].

Tools are available to help optimize for specific cases. The excellent Nvidia CUTLASS library exposes access to many more fine-grained options compared to the standard cuBLAS library. The not faint of heart can try programming Nvidia GPUs at the level of PTX, or (shudder) SASS. Superoptimization might help, but only for very small code fragments and even then there may be too many external factors influencing performance to make it effective.

Autotuning is a promising approach though it doesn’t seem to have reached its full potential in production. AI might really help here [6]; in our own paper we had some success using machine learning methods like decision trees and random forests to model performance as a function of problem size, though our work was exploratory and not production-ready. To make a well-crafted general solution it would seem would require a lot of effort to do right. Code sustainability and maintenance are also critical; a sustainable workflow would be needed to retrain on new GPUs, new CUDA releases and even site-specific and system-specific settings like GPU power and frequency cap policies.

Most recent AI-driven work focuses on optimizing performance for one or a few problem sizes only. A truly production-quality general purpose tool would give both 100% accurate results and also top achievable performance for any input problem size (even for corner cases) or data type. This would require both optimized GPU kernels and optimal kernel dispatcher for kernel selection. And the method would need to be robust to issues like power and frequency variabilities in production runs. This would seem to currently be an unsolved problem. Solving it would be of huge benefit to the hyperscaler community.

Notes

[1] For related work from a slightly different angle, see this excellent work from Matt Sinclair’s lab.

[2] It turned out this study was helpful to us for production runs, to help us to triage an odd performance conundrum we encountered when attempting an exascale run (see here, here).

[3] Incidentally this example shows the hazards of simplistic benchmark suites to measure GPU code performance. Unless the benchmark captures a truly large and varied set of input cases, any new optimization method proposed can artificially “overfit” performance on the tests and still underperform miserably on many user cases of interest.

[4] I once wrote a 1-D wavelet convolution kernel for a Sparc processor, using a circular register buffer and loop unrolling to minimize loads and stores, this achieving near-peak performance. The code was correctly compiled from C to assembly, and performance for a given problem was almost precisely predictable. That was before the days of complex memory hierarchies.

[5] One vendor I know of used to take customer requests for hand tuning expensive library calls and made them run fast at the specific customer problem sizes.

[6] LLM kernel generation seems like a natural fit, particularly since LLM-generated code quality has much improved in recent months. Kernel selection and parameter selection for block size, tiling etc. might be better solved by direct training of machine learning models, or methods like this. Comparative studies on this would be informative.

 

Lessons Learned With the Z3 SAT/SMT Solver

Posted on by Wayne Joubert

Community best practices are useful for helping use a software product more effectively. I’ve just completed a small project using the Z3 solver. Here are some things I’ve learned:

  • My project involves an optimization problem: for a subset of Boolean variables, maximize the count of how many are true. My specific problem is solved much faster with Z3 by converting to a decision problem: set up a base problem to solve for the count being at least a certain fixed number, and iterate using bisection search to find the highest number satisfied. Bisection has been used for this problem before. Also, certain methods may possibly reduce the number of bisection steps.
  • Using Z3  “tactics” can greatly speed up the solve process. I found a good combination of tactics by trial and error, guided in part by the descriptions of the tactics. ChatGPT was of some help in finding good selections to try. An interesting paper discusses use of Monte Carlo tree search to define a good chain of tactics. The branching factor here is high, perhaps around 1000, though there are some redundancies in this number. Training multi-step MCTS might be expensive, but doing this once to get a good static chain of tactics might be worthwhile.
  • The strength of Z3 is in its extremely broad functionality, more so than its raw compute performance. It would be a daunting task for the Z3 team to fully optimize every possible solve option. I examined some of the SMT solver competitions to find faster codes. CVC5 on one case I tried was about twice as fast as Z3; I’ve seen similar reports in the literature. Presently I don’t find it worth the switching costs to use CVC5. One approach might be to use the very capable tactics engine of Z3 and pass the resulting modified problem to CVC5.
  • The specific formulation of the problem can make a big difference in solver performance. I’ve already seen this in the area of iterative linear solvers, for example diagonal matrix scaling can dramatically help (conjugate gradients) or hurt (multigrid) solver performance. Same thing here. Hence the huge importance in good “preprocessing“ for SAT/SMT solvers. One could wish the solver could handle all this automatically without user intervention. However, these powerful tools must be brandished very carefully for maximum effect.
  • Generally, one should move as much of the problem outside of the solver as possible, since the solver is the long pole in the tent in terms of scalability. For example if there is a Z3 integer that must be limited to a certain range and additionally some values in the interval must be blacklisted, it’s better, if possible, to compress all of the valid values into a single interval, to make testing for validity simpler in the Z3 code.
  • Along these lines: the Z3 tactics for propagating constants are not perfect; thus it can help to manually propagate constants (though this unfortunately makes the code more messy). This propagation can also sometimes allow for removal of unneeded constraints, further speeding up performance. Relatedly, some intriguing work by Benjamin Mikek shows how one can use the LLVM code optimizer to optimize the SMT problem in a way that is complementary to Z3 tactics, achieving significant speedup (for more info see here, here and here). I haven’t tried this but it seems promising.
  • Because of the scalability challenge of SMT solvers, various simplifying heuristics to modify the problem can be helpful. For example: solving a subproblem of the main problem and holding the resulting variables fixed in order to solve the rest of the problem. Or solving a simpler, smaller problem first to determine variable presets for the full problem. With these heuristics, one does not in general find the true global optimum; but the result may be adequate.
  • CPU threading does not work for my case (Z3 Python, macOS). Perfect parallelization of SAT and SMP is an unsolved (and perhaps in some sense not fully solvable) problem. One can naïvely parallelize bisection search by converting to trisection, etc., but this does not give perfect speedup (specif., log(P) speedup on P threads). Improvements to parallel bisection in some cases may be possible. Recent work by Armin Biere and colleagues looks promising; as I read it, near perfect speedup up to eight threads (at least for some problems).
  • Some of the main developers of Z3 are on Stack Overflow and have been active in the past answering questions. This seems very useful.

Resources like Handbook of Satisfiability and the proceedings of various SAT/SMT conferences seem helpful. More information on best practices for non-expert practitioners would be a great help to the community. If you know of any good resources, please share in the comments.

On Making Databases Run Faster

Posted on by Wayne Joubert

Database  technology is a mature field, and techniques for optimizing databases are well understood. However, surprises can still happen.

Certain performance optimizations you might expect to be automatic are not really. I’m working with a legacy code developed some time ago, before modern notions of separation of concerns between code business logic and data storage. The code runs slower than you’d expect, and some have wondered as to why this is.

Profiling of the code revealed that the slowdown was not in the core computation, but rather in the reading and writing of the backend database, which occurs frequently when this code executes.

My first thought was to run with the database in RAM disk, which would give higher bandwidth and lower latency than spinning disk or SSD. This helped a little, but not much.

As a short term fix I ended up writing code for (in-memory) hash tables as an interposer between the code and the database. This can cache commonly accessed values and thus reduce database access.

I would’ve thought high-speed RAM caching of values would be default behavior for a database manager. A principle of interface design is to make the defaults as useful as possible. But in this case apparently not.

Thankfully my fix gave over 10X speedup in application launch time and 6X speedup in the core operation of the code.

The project team is moving toward SQLite for database management in the near future. SQLite has perhaps a dozen or so available methods for optimizations like this. However early experiments with SQLite for this case show that more fundamental structural code modifications will also be needed, to improve database access patterns.

As with general code optimization, sometimes you’d be inclined to think the system (compiler, database manager, etc.) will “do it all for you.” But often not.