Math

New Mersenne prime found

Posted on by John

Mersenne numbers have the form 2p − 1. A Mersenne prime is a Mersenne number that is also a prime.

A new Mersenne prime discovery was announced today: 2p − 1 is prime for p = 136279841. The size of the new Mersenne prime is consistent with what was predicted.

For many years now, the largest known prime has been a Mersenne prime. That is because there is an special algorithm for testing whether a Mersenne number is prime, the Lucas-Lehmer test. Because of this algorithm, Mersenne numbers can be tested for primality far more efficiently than can arbitrary numbers of comparable size.

There are now 52 known Mersenne primes, but the number just announced may not be the 52nd Mersenne prime. It has been confirmed that the 2136279841 − 1 is prime, but it has not been confirmed that there are no Mersenne primes between the 51st Mersenne prime and the number just announced. There could be gaps.

If you were to write the latest Mersenne prime in hexadecimal, it would be a 1 followed by 34,069,960 F’s.

Related posts

Channel capacity of a telegraph

Posted on by John

Claude Shannon’s famous paper A Mathematical Theory of Communication [1] includes an example saying that the channel capacity of a telegraph is log2 W where W is the largest real root of the determinant equation

\begin{vmatrix}-1 & W^{-2} + W^{-4} \\ W^{-3} + W^{-6} & W^{-2} + W^{-4} - 1 \end{vmatrix} = 0

Where in the world did that come from?

I’ll sketch where the equation above came from, but first let’s find W and log2 W.

Calculating channel capacity

If you take the determinant and multiply by W10 you get a 10th degree polynomial. A plot shows this polynomial has a root between 1.4 and 1.5.

Applying the bisection method to that interval shows W = 1.4529 and so log2 W = 0.5389 which agrees with the value 0.539 that Shannon gives in his paper. This means that a telegraph can transmit a little more than one bit of information per unit time.

Interpretation

The result above means that a telegraph can transmit a little more than half a bit of information per unit time. But what is the unit of time implicit in Shannon’s example?

We think of Morse code as having two symbols—dot and dash—but in reality it has four symbols: dot, dash, intra-character space, and intra-word space. Shannon assumes that these four symbols take 2, 4, 3, and 6 units of time. Note that the time slice assigned to a dot or a dash includes enough silence at the end to distinguish dots and dashes.

Shannon does not assume that a telegraph is limited to send valid Morse code, only that it can transmit symbols of the four lengths discussed above, and that there are no consecutive spaces. He creates a finite automata model in which an intra-character space or an intra-word space can only transition to a dot or a dash.

Channel capacity

Shannon defines channel capacity in [1] as

C = \lim_{T\to\infty} \frac{\log_2 N(T)}{T}

where N(T) is the number of allowed signals of duration T. The hard part is calculating, or estimating, N(T). In the case of a telegraph, we can image calculating N(T) recursively via

N(t) = N(t - t_1) + N(t - t_2) + N(t - t_3) + N(t - t_4)

where the t‘s with subscripts are the times required to transmit each of the four possible symbols. The four terms on the right side consider the possibilities that the symbol transmitted immediately before time t is a dot, dash, intra-character space, or intra-word space.

The equation for N(t) is a finite difference equation, and so the asymptotic behavior of the solution is well known. Since we’re taking a limit as T goes to infinity, we only need to know the asymptotic behavior, so this works out well.

If you squint at the determinant at the top of the post, it looks sorta like an eigenvalue calculation, as hinted at by the −1 terms on the diagonal. And in fact that is what is going on. There’s an eigenvalue problem hidden in there that describes the asymptotic behavior of the difference equation.

Shannon’s theorem

Here is Theorem 1 from Shannon’s paper.

Let bij(s) be the duration of the sth symbol which is allowable in state i and leads to state j. The channel capacity C is equal to log2 W where W is the largest real root of the determinant equation

\left| \sum_s W^{-b_{ij}^{(s)}} - \delta_{ij} \right| = 0

where δij = 1 if i = j and is zero otherwise.

This theorem accounts for the determinant at the top of the post. It’s a 2 by 2 determinant because Shannon’s model of a telegraph is a finite automaton with two states, depending on whether the preceding symbol was or was not a space.

Related posts

[1] Claude Shannon. A Mathematical Theory of Communication. The Bell System Technical Journal, Vol. 27, pp. 379–423, July, October, 1948.

Squares, triangles, and octal

Posted on by John

I ran across the following theorem in Ross Honsberger’s book Mathematical Morsels:

Every odd square ends in 1 in base 8, and if you cut off the 1 you have a triangular number.

A number is an odd square if and only if it is the square of an odd number, so odd squares have the form (2n + 1)².

Both parts of the theorem above follow from the calculation

( (2n + 1)² − 1 ) / 8 = n(n + 1) / 2.

In fact, we can strengthen the theorem. Not only does writing the nth odd square in base 8 and chopping off the final digit give some triangular number, it gives the nth triangular number.

Triangle circle maximization problem

Posted on by John

Let a, b, and c be the sides of a triangle. Let r be the radius of an inscribed circle and R the radius of a circumscribed circle. Finally, let p be the perimeter. Then the previous post said that

2prR = abc.

We could rewrite this as

2rR = abc / (a + b + c)

The right hand side is maximized when a = b = c. To prove this, maximize abc subject to the constraint a + b + c = p using Lagrange multipliers. This says

[bc, ac, ab] = λ[1, 1, 1]

and so ab = bc = ac, and from there we conclude a = b = c. This means among triangles with any given perimeter, the product of the inner and outer radii is maximized for an equilateral triangle.

The inner radius for an equilateral triangle is (√3 / 6)a and the outer radius is a/√3, so the maximum product is a²/6.

Related posts

Why does FM sound better than AM?

Posted on by John

The original form of radio broadcast was amplitude modulation (AM). With AM radio, the changes in the amplitude of the carrier wave carries the signal you want to broadcast.

AM signal

Frequency modulation (FM) came later. With FM radio, changes to the frequency of the carrier wave carry the signal.

I go into the mathematical details of AM radio here and of FM radio here.

Pinter [1] gives a clear explanation of why the inventor of FM radio, Edwin Howard Armstrong, correctly predicted that FM radio transmissions would be less affected by noise.

Armstrong reasoned that the effect of random noise is primarily to amplitude-modulate the carrier without consistently producing frequency derivations.

In other words, noise tends to be a an unwanted amplitude modulation, not a frequency modulation.

FM radio was able to achieve levels of noise reduction that people steeped in AM radio thought would be impossible. As J. R. Carson eloquently but incorrectly concluded

… as the essential nature of the problem is more clearly perceived, we are unavoidably forced to the conclusion that static, like the poor, will always be with us.

But as Pinter observes

The substantial reduction of noise in a FM receiver by use of a limiter was indeed a startling discovery, contrary to the behavior of AM systems, because experience with such systems had shown that the noise contribution to the modulation of the carrier could not be eliminated without partial elimination of the message.

Related posts

[1] Philip F. Pinter. Modulation, Noise, and Spectral Analysis. McGraw-Hill 1965.

Shifted reciprocal

Posted on by John

It’s interesting to visualize functions of a complex variable, even very simple functions like f(z) = 1/z. The previous post looked at what happens to triangles under the reciprocal map w = 1/z. This post will look at the same map applied to a polar grid, then look at the effect a shift has, replacing 1/z with 1/(z − c).

The function 1/z is a Möbius transformation, and so it maps lines and circles to lines and circles. And in the case of a polar grid, lines go to lines and circles go to circles. The overall grid is unchanged, even though circles swap places with other circles, and lines swap places with other lines. To see this, note that

1/reiθ = (1/r)e−iθ

This means that the function 1/z maps a circle of radius r to a circle of radius 1/r, and it maps a line of slope m to a line of slope −1/m.

Things get more interesting when we shift the reciprocal function to w = 1/(z − c). Now lines will map to circles, unless the line passes through c. Circles will still map to circles, unless the circle passes through c, but we won’t have circles swapping places because the function 1/(z − c) is not its own inverse, unlike 1/z. Here’s a plot with c = 0.1.

Note that circles map to circles, but the center of a circle does not necessarily map to the center of the image circle. So the green circles in the z-plane map to green circles in the w-plane, but the circles in the z-plane are concentric while their images in the w-plane are not.

The blue lines in the z-plane become blue circles in the w-plane, though some of the circles are too large to fit in the frame of the plot.

As we discussed in the previous post, Möbius transformations are easier to discuss if you adjoint a point at infinity to the complex plane. The radial lines in the z-plane all meet at ∞, and so their images in the w-plane all meet at 1/(∞ – c) = 0.

One final thing to note is that however small ε > 0 is, the images of the grid lines are very different under 1/(z − ε) compared to 1/z. Individual z‘s that start out close together are mapped to w‘s that are close together, but the images of the system of lines and circles is qualitatively different for ε > 0 versus ε = 0.

Related posts

Triangles to Triangles

Posted on by John

The set of functions of the form

f(z) = (az + b)/(cz + d)

with ad ≠ bc are called bilinear transformations or Möbius transformations. These functions have three degrees of freedom—there are four parameters, but multiplying all parameters by a constant defines the same function—and so you can uniquely determine such a function by picking three points and specifying where they go.

Here’s an explicit formula for the Möbius transformation that takes z1, z2, and z3 to w1, w2, and w3.

\begin{vmatrix} 1 & z & w & zw \\ 1 & z_1 & w_1 & z_1w_1 \\ 1 & z_2 & w_2 & z_2w_2 \\ 1 & z_3 & w_3 & z_3w_3 \\ \end{vmatrix} = 0

To see that this is correct, or at least possible, note that if you set z = zi and w = wi for some i then two rows of the matrix are equal and so the determinant is zero.

Triangles, lines, and circles

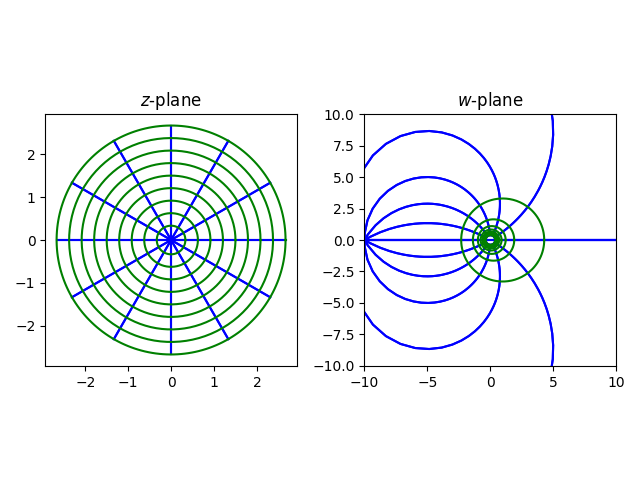
You can pick three points in one complex plane, the z-plane, and three points in another complex plane, the w-plane, and find a Möbius transformation w = f(z) taking the z-plane to the w-plane sending the specified z‘s to the specified w‘s.

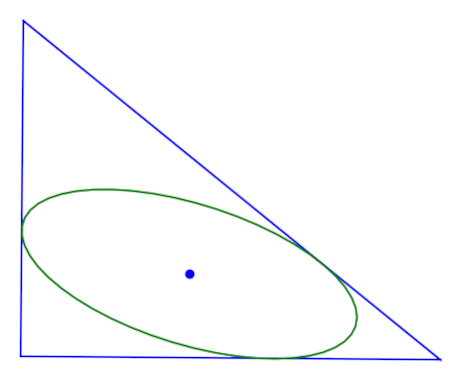
If you view the three points as vertices of a triangle, you’re specifying that one triangle gets mapped to another triangle. However, the sides of your triangle may or may not be straight lines.

Möbius transformations map circles and lines to circles and lines, but a circle might become a line or vice versa. So the straight lines of our original triangle may map to straight lines or they may become circular arcs. How can you tell whether the image of a side of a triangle will be straight or curved?

When does a line map to a line?

It’ll be easier if we add a point ∞ to the complex plane and think of lines as infinitely big circles, circles that pass through ∞.

The Möbius transformation (az + b)/(cz + d) takes ∞ to a/c and it takes −d/c to ∞.

The sides of a triangle are line segments. If we look at the entire line, not just the segment, then this line is mapped to a circle. If this line contains the point that gets mapped to ∞ then the image of the line is an infinite circle (i.e. a line). Otherwise the image of the line is a finite circle.

The line between z1 and  z2 can be parameterized by

z1 + t(z2 − z1)

where t is real. So the image of this line will be a line if and only if

z1 + t(z2 − z1) = −d/c

for some real t. So solve for t and see whether you get a real number.

Note that if the point that is mapped to ∞ lies inside the line segment, not just on the line, then the image of that side of the triangle is infinitely long.

Examples

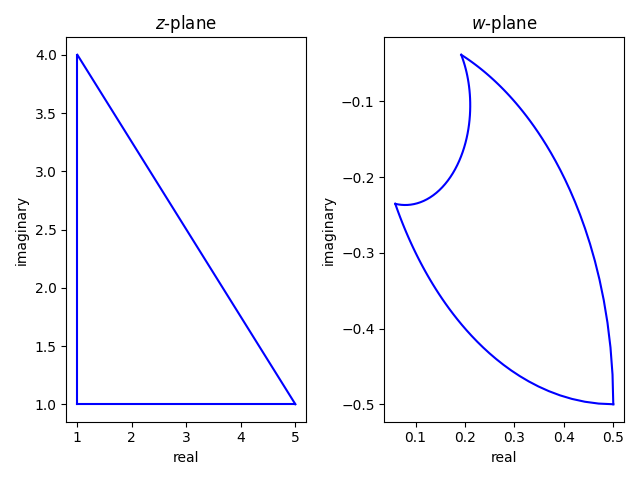
To keep things as simple as possible without being trivial, we’ll use the Möbius transformation f(z) = 1/z. Clearly the origin is the point that is mapped to ∞. The side of a triangle is mapped to a straight line if and only if the side is part of a line through the origin.

First let’s look at the triangle with vertices at (1, 1), (1, 4), and (5, 1). None of the sides is on a line that extends to the origin, so all sides map to circular arcs.

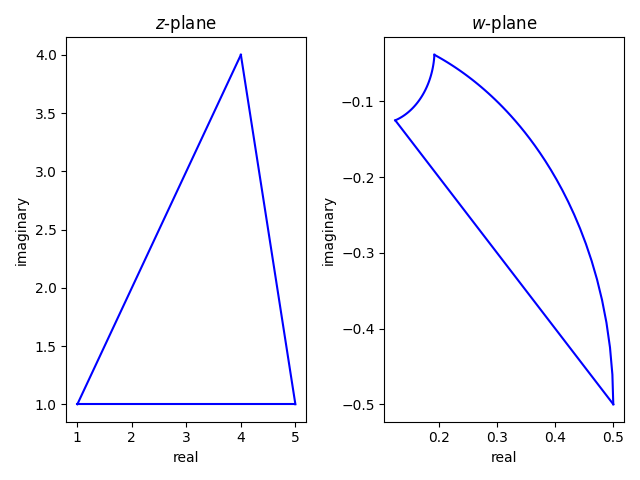
Next let’s move the second point from (1, 4) to (4, 4). The line running between (1, 1) and (4, 4) goes through the origin, and so the segment along that line maps to a straight line.

Related posts

Golden ellipse

Posted on by John

A golden ellipse is an ellipse whose axes are in golden proportion. That is, the ratio of the major axis length to the minor axis length is the golden ratio φ = (1 + √5)/2.

Draw a golden ellipse and its inscribed and circumscribed circles. In other words draw the largest circle that can fit inside and the smallest circle outside that contains the ellipse.

Then the area of the ellipse equals the area of the annulus bounded by the two circles. That is, the area of the green region

equals the area of the orange region.

The proof is straight forward. Let a be the semimajor axis and b the semiminor axis, with a = φb.

Then the area of the annulus is

π(a² − b²) = πb²(φ² − 1).

The area of the ellipse is

πab = πφb².

The result follows because the golden ratio satisfies

φ² − 1 = φ.

Related posts

Areal coordinates and ellipse area

Posted on by John

Barycentric coordinates are sometimes called area coordinates or areal coordinates in the context of triangle geometry. This is because the barycentric coordinates of a point P inside a triangle ABC correspond to areas of the three triangles PBC, PCA and PAB.

(This assumes ABC has unit area. Otherwise divide the area of each of the three triangles by the area of ABC. We will assume for the rest of this post that the triangle ABC has unit area.)

Areal coordinates take three numbers two describe a point in two dimensional space. Why would you do that? It’s often useful to use an overdetermined coordinate system. The benefit of adding one more coordinate is that you get a coordinate system matched to the geometry of the triangle. For example, the vertices of the triangle have coordinates (1, 0, 0), (0, 1, 0), and (0, 0, 1), regardless of the shape of the triangle.

Here is an example of a theorem [1] that is convenient to state in terms of areal coordinates but that would be more complicated in Cartesian coordinates.

First we need to define the midpoint triangle, also called the medial triangle. This is the triangle whose vertices are the midpoints of each side of ABC. In terms of areal coordinates, the vertices of this triangle are (0, ½, ½), (½, 0, ½), and (½, ½, 0).

Now let P be any point inside the midpoint triangle of ABC. Then there is a unique ellipse E inscribed in ABC and centered at P.

Let (α, β, γ) be the areal coordinates of P. Then the area of E is

\pi \sqrt{(1 - 2\alpha)(1 - 2\beta)(1 - 2\gamma)}

Because P is inside the medial triangle, each of the areal coordinates are less than ½ and so the quantity under the square root is positive.

Finding the equation of the inscribed ellipse is a bit complicated, but that’s not necessary in order to find its area.

Related posts

[1] Ross Honsberger. Mathematical Plumbs. 1979