A few months ago I wrote about several equations that come up in geometric calculations that all have the form of a determinant equal to 0, where one column of the determinant is all 1s.

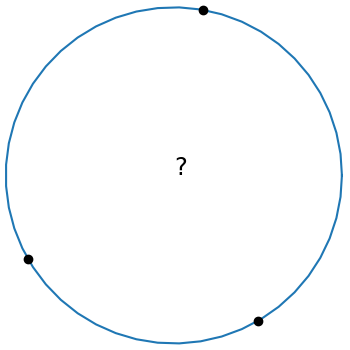
The equation of a circle through three points (x₁, y₁), (x₂, y₂), and (x₃, y₃) has this form:

This is elegant equation, but it’s not in a form that’s ready to program. This post will start with the equation above and conclude with code.

Let M_ij be the determinant of the minor of the (i, j) element of the matrix above. That is, M_ij is the determinant of the 3 × 3 matrix obtained by deleting the ith row and jth column. Then we can expand the determinant above by minors of the last column to get

which we can rewrite as

A circle with center (x₀, y₀) and radius r₀ has equation

By equating the coefficients x and y in the two previous equations we have

Next we expand the determinant minors in more explicit form.

Having gone to the effort of finding a nice expression for M₁₁ we can reuse it to find M₁₂ by the substitution

as follows:

And we can find M₁₃ from M₁₂ by reversing the role of the xs and ys.

Now we have concrete expressions for M₁₁, M₁₂, and M₁₃, and these give us concrete expressions for x₀ and y₀.

To find the radius of the circle we simply find the distance from the center (x₀, y₀) to any of the points on the circle, say (x₁, y₁).

The following Python code incorporates the derivation above.

    def circle_thru_pts(x1, y1, x2, y2, x3, y3):
        s1 = x1**2 + y1**2
        s2 = x2**2 + y2**2
        s3 = x3**2 + y3**2
        M11 = x1*y2 + x2*y3 + x3*y1 - (x2*y1 + x3*y2 + x1*y3)
        M12 = s1*y2 + s2*y3 + s3*y1 - (s2*y1 + s3*y2 + s1*y3)
        M13 = s1*x2 + s2*x3 + s3*x1 - (s2*x1 + s3*x2 + s1*x3)
        x0 =  0.5*M12/M11
        y0 = -0.5*M13/M11
        r0 = ((x1 - x0)**2 + (y1 - y0)**2)**0.5
        return (x0, y0, r0)

The code doesn’t use any loops or arrays, so it ought to be easy to port to any programming language.

For some inputs the value of M₁₁ can be (nearly) zero, in which case the three points (nearly) lie on a line. In practice M₁₁ can be nonzero and yet zero for practical purposes and so that’s something to watch out for when using the code.

The determinant at the top of the post is zero when the points are colinear. There’s a way to make rigorous the notion that in this case the points line on a circle centered at infinity.

Update: Equation of an ellipse or hyperbola through five points

A few years ago I wrote several posts about “squircles”, starting with this post. These are shapes satisfying

where typically p = 4 or 5. The advantage of a squircle over a square with rounded edges is that the curvature varies continuously around the figure rather than jumping from a constant positive value to zero.

Manuel Fernández-Guasti developed a slightly different shape also called a squircle but with a different equation

We need to give separate names to the two things called squircles, and so I’ll name them after their parameters: p-squircles and s-squircles.

As s varies from 0 to 1, s-squircles change continuously from a circle to a square, just as p-squircles varies do as p goes from 2 to ∞.

The two kinds of squircles are very similar. Here’s a plot of one on top of the other. I’ll go into detail later of how this plot was made.

Advantage of s-squircles

The equation for a p-squircle is polynomial if p is an even integer, but in general the equation is transcendental. The equation for an s-squircle is a polynomial of degree 4 for all values of s. It’s more mathematically convenient, and more computationally efficient, to have real numbers as coefficients than as exponents. The s-squircle is an algebraic variety, the level set of a polynomial, and so can be studied via algebraic geometry whereas p-squircles cannot (unless p is an even integer).

It’s remarkable that the two kinds of squircles are so different in the structure of their defining equation and yet so quantitatively close together.

Equal area comparison

I wanted to compare the two shapes, so I plotted p-squircles and s-squircles of the same area.

The area of a p-squircle is given here where n = 2. The area of an s-squircle is given here MathWorld where k = 1.

Here E is the “elliptic integral of the second kind.” This function has come up several times on the blog, for example here.

Both area function are increasing functions of their parameters. We have A₁(2) = A₂(0) and A₁(∞) = A₂(1). So we can pick a value of p and solve for the corresponding value of s that gives the same area, or vice versa.

The function A₁ can be implemented in Mathematica as

    A1[p_] := 4 Gamma[1 + 1/p]^2/Gamma[1 + 2/p]

The function A₂ is little trickier because Mathematica parameterizes the elliptic integral slightly differently than does the equation above.

    A2[s_] := 4 EllipticE[ArcSin[s], s^-2]/s

Now I can solve for the values of s that give the same area as p = 4 and p = 5.

    FindRoot[A2[s] == A1[4], {s, 0.9}]

returns 0.927713 and

    FindRoot[A2[s] == A1[5], {s, 0.9}]

returns 0.960333. (The 0.9 argument in the commands above is an initial guess at the root.)

The command

    ContourPlot[{x^2 + y^2 == 0.927713 ^2 x^2 y^2 + 1, 
        x^4 + y^4 == 1}, {x, -1, 1}, {y, -1, 1}]

produces the following plot. This is the same plot as at the top of the post, but enlarged to show detail.

The command

    ContourPlot[{x^2 + y^2 == 0.960333 ^2 x^2 y^2 + 1, 
        Abs[x]^5 + Abs[y]^5 == 1}, {x, -1, 1}, {y, -1, 1}]

produces this plot

In both cases the s-squircle is plotted in blue, and the p-squircle in gold. The gold virtually overwrites the blue. You have to look carefully to see a little bit of blue sticking out in the corners. The two squircles are essentially the same to within the thickness of the plotting lines.

History

The term “squircle” goes back to 1953, but was first used as it is used here around 1966. More on this here.

However, Fernández-Guasti was the first to use the term in scholarly literature in 2005. See the discussion in the MathWorld article.