There’s an ancient saying “Whom the gods would destroy they first make mad.” (Mad as in crazy, not mad as in angry.) I wrote a variation of this on Twitter:
Whom the gods would destroy, they first give real-time analytics.
Having more up-to-date information is only valuable up to a point. Past that point, you’re more likely to be distracted by noise. The closer you look at anything, the more irregularities you see, and the more likely you are to over-steer [1].
I don’t mean to imply that the noise isn’t real. (More on that here.) But there’s a temptation to pay more attention to the small variations you don’t understand than the larger trends you believe you do understand.
I became aware of this effect when simulating Bayesian clinical trial designs. The more often you check your stopping rule, the more often you will stop [2]. You want to monitor a trial often enough to shut it down, or at least pause it, if things change for the worse. But monitoring too often can cause you to stop when you don’t want to.
Flatter than glass
A long time ago I wrote about the graph below.
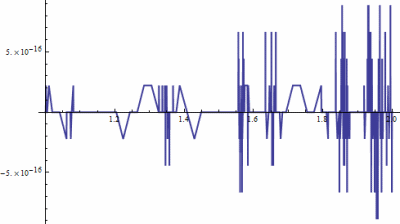
The graph looks awfully jagged, until you look at the vertical scale. The curve represents the numerical difference between two functions that are exactly equal in theory. As I explain in that post, the curve is literally smoother than glass, and certainly flatter than a pancake.
Notes
[1] See The Logic of Failure for a discussion of how over-steering is a common factor in disasters such as the Chernobyl nuclear failure.
[2] Bayesians are loathe to talk about things like α-spending, but when you’re looking at stopping frequencies, frequentist phenomena pop up.

I’ve always wondered if there’s a way to design a stopping rule that works under continuous observation. It seems like it would be possible, kinda like how e can be used to calculate continuous interest accumulation which is based on a discrete computation. This is what I’d want for my impatient boss (and self).
I’ve implemented continuous stopping rules.
John D. Cook. Continuous safety monitoring in single-arm, time-to-event trials without software (2005). Technical Report UTMDABTR-006-05.
https://www.johndcook.com/UTMDABTR-006-05.pdf
John D. Cook. Simulation results for phase II clinical trial durations (2004). Technical Report UTMDABTR-014-04
https://www.johndcook.com/UTMDABTR-014-04.pdf
Valen E. Johnson, John D. Cook. Bayesian Design of Single-Arm Phase II Clinical Trials with Continuous Monitoring. Clinical Trials 2009; 6(3):217–26.
Interesting, thank you for the references! I look forward to reviewing them when I have more attention. To relate it into a more mundane topic, I assume this is similar to deciding when to stop an ongoing A/B test, is that true? (Ignoring the multitude other experimental design flaws that commonly inflict A/B tests.)
If you have binary outcomes (e.g. toxic or not toxic) then clinical trials are like an A/B test. When you have time outcomes (e.g. survival time) they’re a little different; web tests are usually binary rather than the time to an event. I suppose you could track time on page, for example.
As a guide, I think “real-timeness” can be bound to the physical world: people are making decisions at that rate – and if measurement digress they interfere (like heart rate) or moving goods “at that rate” and if measurement indicates they redirect – gas or energy will be best examples. Extension of the thought would be that the market is trading at a subsecond interval is trading on noise.
One of my teacher told me to have a model in mind, even if it’s incorrect or inaccurate relative to the data, as a frame of reference, to drive one to look at the bigger picture, and also to learn, especially if your initial mental model turned out to be incorrect. My only concern at the time is this may bias me to a conclusion, but if one is open to let the data speak for itself, it tends to damp the chance of bias. What is your opinion of this process? What I found is in school the initial phase, e.g., clear problem statement, got glossed over with nice and clean examples, rather than the messy real world shock one experienced once one enters a work setting. I just I’m repeating 1 of your recent blogs.