Claude Shannon’s famous paper A Mathematical Theory of Communication [1] includes an example saying that the channel capacity of a telegraph is log2 W where W is the largest real root of the determinant equation
Where in the world did that come from?
I’ll sketch where the equation above came from, but first let’s find W and log2 W.
Calculating channel capacity
If you take the determinant and multiply by W10 you get a 10th degree polynomial. A plot shows this polynomial has a root between 1.4 and 1.5.
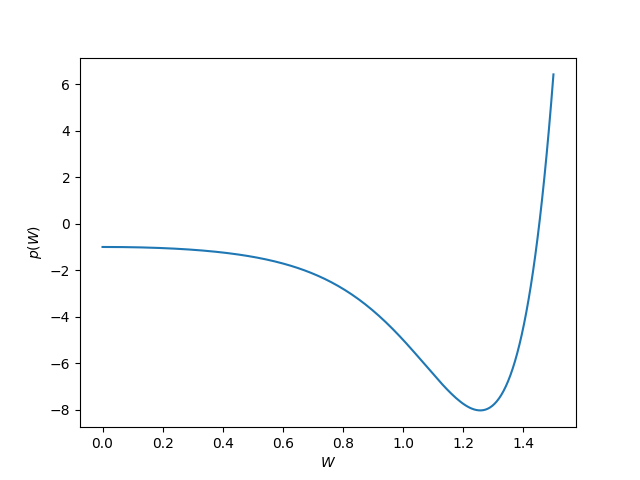
Applying the bisection method to that interval shows W = 1.4529 and so log2 W = 0.5389 which agrees with the value 0.539 that Shannon gives in his paper. This means that a telegraph can transmit a little more than one bit of information per unit time.
Interpretation
The result above means that a telegraph can transmit a little more than half a bit of information per unit time. But what is the unit of time implicit in Shannon’s example?
We think of Morse code as having two symbols—dot and dash—but in reality it has four symbols: dot, dash, intra-character space, and intra-word space. Shannon assumes that these four symbols take 2, 4, 3, and 6 units of time. Note that the time slice assigned to a dot or a dash includes enough silence at the end to distinguish dots and dashes.
Shannon does not assume that a telegraph is limited to send valid Morse code, only that it can transmit symbols of the four lengths discussed above, and that there are no consecutive spaces. He creates a finite automata model in which an intra-character space or an intra-word space can only transition to a dot or a dash.
Channel capacity
Shannon defines channel capacity in [1] as
where N(T) is the number of allowed signals of duration T. The hard part is calculating, or estimating, N(T). In the case of a telegraph, we can image calculating N(T) recursively via
where the t‘s with subscripts are the times required to transmit each of the four possible symbols. The four terms on the right side consider the possibilities that the symbol transmitted immediately before time t is a dot, dash, intra-character space, or intra-word space.
The equation for N(t) is a finite difference equation, and so the asymptotic behavior of the solution is well known. Since we’re taking a limit as T goes to infinity, we only need to know the asymptotic behavior, so this works out well.
If you squint at the determinant at the top of the post, it looks sorta like an eigenvalue calculation, as hinted at by the −1 terms on the diagonal. And in fact that is what is going on. There’s an eigenvalue problem hidden in there that describes the asymptotic behavior of the difference equation.
Shannon’s theorem
Here is Theorem 1 from Shannon’s paper.
Let bij(s) be the duration of the sth symbol which is allowable in state i and leads to state j. The channel capacity C is equal to log2 W where W is the largest real root of the determinant equation
where δij = 1 if i = j and is zero otherwise.
This theorem accounts for the determinant at the top of the post. It’s a 2 by 2 determinant because Shannon’s model of a telegraph is a finite automaton with two states, depending on whether the preceding symbol was or was not a space.
Related posts
[1] Claude Shannon. A Mathematical Theory of Communication. The Bell System Technical Journal, Vol. 27, pp. 379–423, July, October, 1948.
