Ramanujan discovered an incredibly accurate approximation for the perimeter of an ellipse. This post will illustrate how accurate the approximation is and push its limits.
As with all computations involving ellipses, the error of Ramanujan’s approximation increases as eccentricity increases. But the error increases slowly, asymptotically approaching an upper bound that is remarkably small.
Let a and b be the semi-major and semi-minor axes of an ellipse. Then Ramanujan’s approximation for the perimeter of the ellipse is
where λ = (a − b)/(a + b).
Example
To illustrate how accurate the approximation is, let’s apply it to a very large, highly eccentric ellipse: the orbit of Sedna, a dwarf planet discovered in 2003. Sedna has the most elliptical orbit of any of the dwarf planets, 0.8496 compared to 0.2488 for Pluto. Sedna is also about 12 times further from the sun than Pluto.
The semi-major axis of Sedna’s orbit is 76 billion kilometers. Eccentricity e corresponds to aspect ratio √(1 − e²) (see this post), and so the semi-minor axis is about 40 billion kilometers. Let’s assume the orbit of Sedna is perfectly elliptical, which it is not, and that the semi-axes stated above are exact, which they are not. Then the length of Sedna’s orbit is on the order of 366 billion kilometers, and Ramanujan’s approximation has an error of about 53 kilometers.
Error
Here’s a plot of the relative error when b = 1 and a varies.
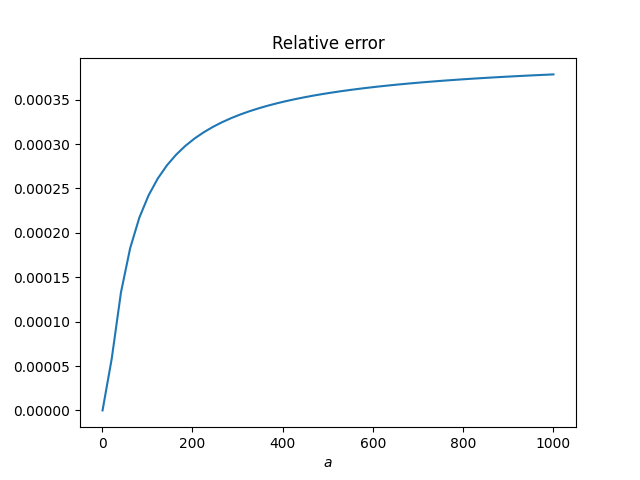
The error appears to be approaching an asymptote, and in fact it is. The error is bound by 4/π − 14/11 = 0.00051227…., as proved here.

Though I’m certain this was mentioned in prior posts, I’m always stunned when seeing the complexity this 2D perimeter approximation then comparing it to the 3D area of a rotated ellipse being simply πab.
My mind intuitively expects 3D (and higher dimensions) to be “harder” than 2D (because the problem/solution space seems so much larger), hence the delight when the reverse is true. Similarly, there are 2D problems whose solution/proof is greatly simplified by working in higher dimensions. Here’s a good collection of examples: https://mathoverflow.net/questions/106705/2d-problems-which-are-easier-to-solve-in-3d
Makes me think of Liouville’s trick for computing the Gaussian integral. He turns a 1-dimensional integral into a 2-dimensional integral and switches to polar coordinates, all so he can insert the r dr term that makes the integral easy.