In the previous post I said that you could define the inverse sine as the function that gives the arc length along a circle, then define sine to be the inverse of the inverse sine. The purpose of such a backward definition is that it generalizes to other curves besides the circle. For example, it generalizes to the lemniscate, a curve studied by Bernoulli.
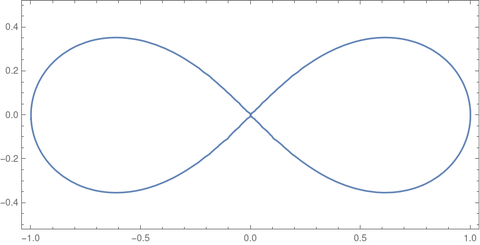
The leminiscate in rectangular coordinates satisfies
and in polar coordinates
The function arcsl(x), analogous to arcsin(x), is defined as the length of the arc along the leminiscate from the origin to the point (x, y). The length of the arc from (x, y) to the x-axis is arccl(x).
The lemniscate sine, sl, is the inverse of arcsl, and the lemniscate cosine, cl, is the inverse of arccl. These functions were first studied by Giulio Fagnano three centuries ago.
The lemniscate functions sl and cl are elliptic functions, and so they have a lot of nice properties and satisfy a lot of identities. See Wikipedia, for example. Update: see this follow up post on addition theorems.
Lemniscate constant
As mentioned in the previous post, generalizations of the sine and cosine functions have corresponding generalizations of π.
Just as the period of sine and cosine is 2π, the period of lemninscate sine and lemniscate cosine is 2ϖ.
The number ϖ is called the lemniscate constant. It is written with Unicode character U+03D6, GREEK SMALL LETTER OMEGA PI. The LaTeX command is \upvarpi.
The lemnmiscate constant ϖ is related to Gauss’ constant G by ϖ = πG.
The area of a squircle is √2 ϖ.
There is also a connection to the beta function: 2ϖ = B(1/4, 1/2).
