Literal alphabets
Natural language alphabets are all within an order of magnitude of the size of the Roman alphabet. The Hebrew alphabet has a few less letters and Russian has a few more. The smallest alphabet I’m aware of is Hawaiian with 13 letters.
Syllabaries are larger than alphabets, but not an order of magnitude larger. For example, Japanese uses 46 symbols and the Cherokee uses 85.
There is a tradeoff between alphabet size and word size that constrains alphabets to be roughly the same size in every culture.
Metaphorical alphabets
Computer science generalizes the term alphabet to mean any fixed collection of symbols and generalizes word to mean any finite sequence of symbols from an alphabet. So, for example, the digits 0 through 9 form an alphabet in this sense, and the words are numbers.
Numbers are sometimes written using smaller or larger alphabets. Binary notation uses an alphabet of only 2 symbols, but numbers require significantly more symbols to express than they do in decimal. Hexadecimal uses an alphabet of 16 symbols and is more compact than decimal notation.
Tradeoffs
Many design problems can be formulated as a tradeoff between alphabet length and word length. I was working on such a problem recently, which motivated this blog post.
Larger alphabets mean shorter words, but a linear reduction in word size requires an exponential increase in alphabet size. For example, we could write numbers using half as many digits if we thought in base 100 and had symbols for numbers 0 through 99. Or we could think in base 1000, increasing the number of digits by a factor of 100 and reducing the length of number representations by a factor of 3.
Word length is inversely proportional to the logarithm of alphabet size, and so if we have some cost proportional to alphabet size a and another cost proportional to word length, the optimal alphabet size for the sum of these costs would minimize
C1a + C2 / log a.
We could divide this objective function by C1 and set w = C1/C2 to simplify the objective to minimizing
a + w / log a
Setting the derivative with respect to a to zero shows that the optimal alphabet size a is given by solving
a (log a)² = w.
As the weight w given to the cost of word size increases, the optimal alphabet size increases as well. A wide range of weights corresponds to a narrower range of alphabet sizes.
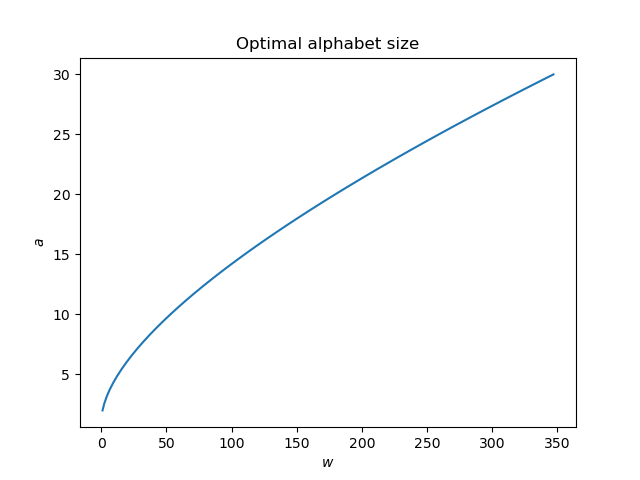
This plot could be misleading. The graph is not showing the cost associated with various alphabet sizes but rather the optimal alphabet size for a given word size cost. The weight w is fixed in any particular application.
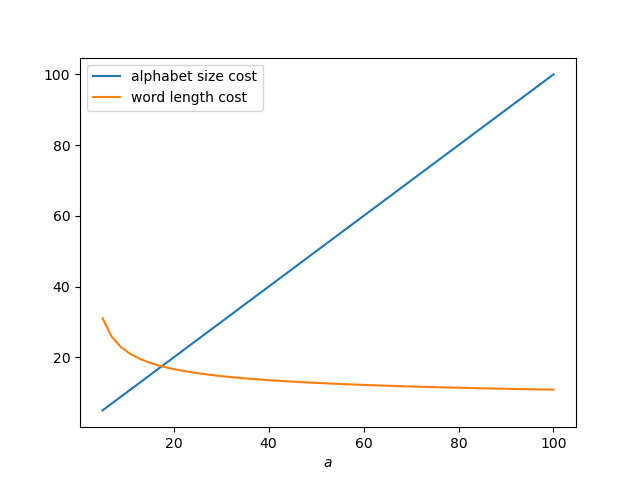
An alphabet of size 10 is optimal for a word length cost weight w of about 50. Using w = 50, the following plot shows how alphabet size cost and word size costs compare. A large increase in alphabet size cost only buys a small decrease in word size cost.
Related post: The base with the largest decibel

A long time ago I saw a similar cost function used to “prove” that ternary is the “best” base. Instead of using an additive cost (which favors larger bases as the expected size of the numbers you have to represent increases), they simply defined the cost as alphabet size multplied by word size. This leads to minimizing a / ln a, which has a minimum at e, and among the integers (since base e is a bit impractical) it has a minimum at 3.
Now in reality this line of argument is pretty weak. Choosing from among “a” symbols doesn’t require “a” units of work for each symbol you encounter. In fact, it’d be more reasonable to say that it’s log a, in which case we come to one of two conclusions:
1. That all bases are fundamentally equal, because it’s the same information no matter what you do, or
2. That binary is the best, because we need to use a whole number of symbols to represent each number, and binary minimizes the “chunking loss” by having the least information per symbol. Plus it has obvious practical advantages in electronic computing.
The modern Rotokas alphabet has only 12 letters. I believe it’s the only alphabet that is a subset of US-ASCII.