In the latest two posts, we have needed to find the percentage points for a chi square random variable when the parameter ν, the number of degrees of freedom, is large.
In Volume 2 of Knuth’s magnum opus TAOCP, he gives a table of percentage points for the chi square distribution for small values of ν and he gives an asymptotic approximation to be used for values of ν > 30.
Knuth’s series is
where xp is the corresponding percentage point function for a normal random variable. Knuth gives a few values of xp in his table.
What Knuth calls xp, I called p in the previous post. The approximation I gave, based on Fisher’s transformation to make the chi squared more like a normal, is similar to Knuth’s series, but not the same.
So which approximation is better? Where does Knuth’s approximation come from?
Comparing approximations
We want to find the quantiles for χ²(100) for p = 0.01 through 0.99. Both Fisher’s approximation and Knuth’s approximation are good enough that it’s hard to tell the curves apart visually when the exact values are plotted along with the two approximations.
But when you subtract off the exact values and just look at the errors, it’s clear that Knuth’s approximation is much better in general.
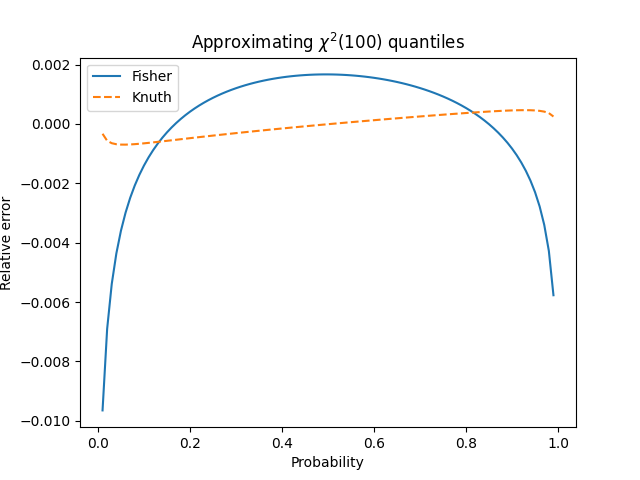
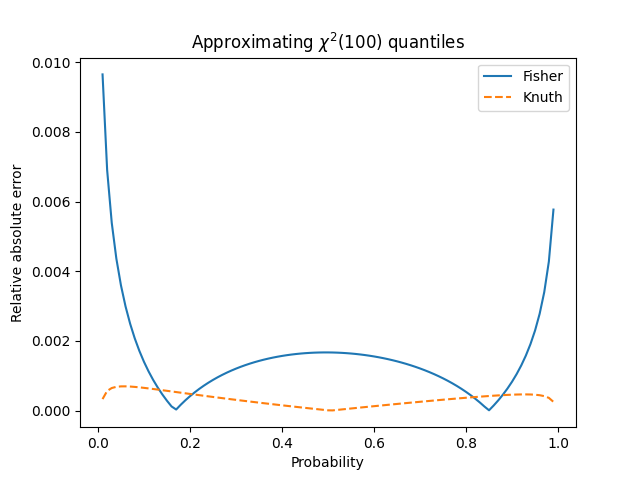
Here’s another plot, taking the absolute value of the error. This makes it easier to see little regions where Fisher’s approximation happens to be better.
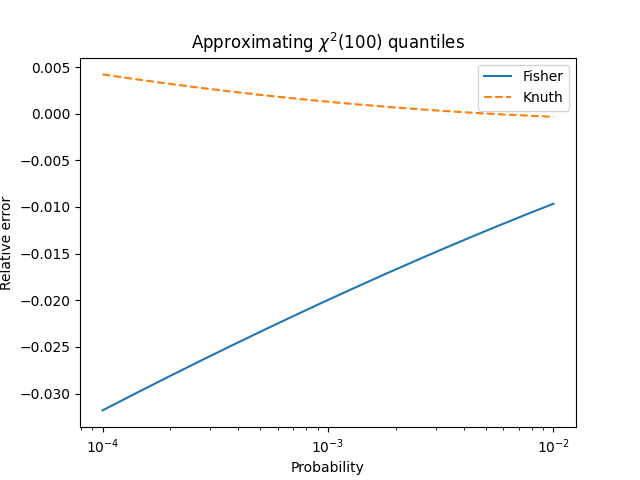
Here are a couple more plots comparing the approximations at more extreme probabilities. First the left tail:
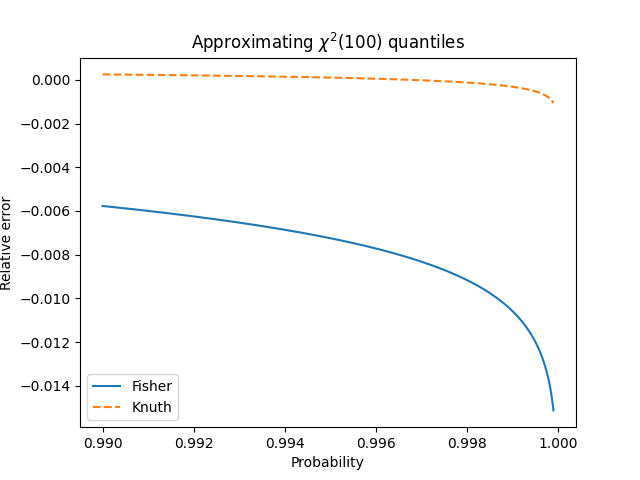
And then the right tail:
Derivation
The table mentioned above says to see exercise 16 in the same section, which in turn refers to Theorem 1.2.11.3A in Volume 1 of TAOCP. There Knuth derives an asymptotic series which is not directly the one above, but does most of the work. The exercise asks the reader to finish the derivation.
