Number of ways to partition a convex polygon

In this post we want to count the number of ways to divide a regular polygon [1] into triangles by connecting vertices with straight lines that do not cross.

Squares

For a square, there are two possibilities: we either connect the NW and SE corners,

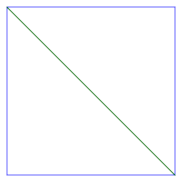
or we connect the SW and NE corners.

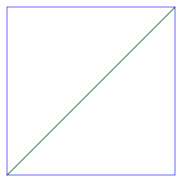
Pentagons

For a pentagon, we pick one vertex and connect it to both non-adjacent vertices.

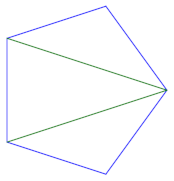
We can do this for any vertex, so there are five possible triangulations. All five triangulations are rotations of the same triangulation. What if we consider these rotations as equivalent? We’ll get to that later.

Hexagons

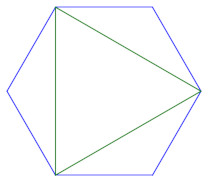
For a hexagon, things are more interesting. We can again pick any vertex and connect it to all non-adjacent vertices, giving six triangulations.

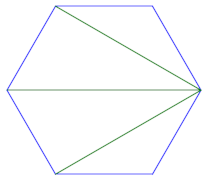
But there are more possibilities. We could connect every other vertex, creating an equilateral triangle inside. We can do this two ways, connecting either the even-numbered vertices or the odd-numbered vertices. Either triangulation is a rotation of the other.

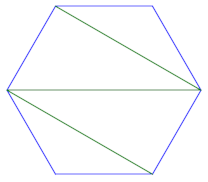
We can also connect the vertices in a zig-zag pattern, creating an N-shaped pattern inside. We could also rotate this triangulation one or two turns. (Three turns gives us the same pattern again.)

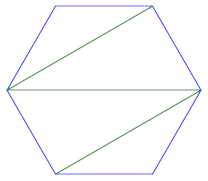
Finally, we could also connect the vertices creating a backward N pattern.

General case

So to recap, we have 2 ways to triangulate a square, 5 ways to triangulate a pentagon, and 6 + 2 + 3 + 3 = 14 ways to triangulate a hexagon. Also, there is only 1 way to triangulate a triangle: do nothing.

Let C_n be the number of ways to triangulate a regular (n + 2)-gon. Then we have C₁ = 1, C₂ = 2, C₃ = 5, and C₄ = 14.

In general,

$C_n = \frac{1}{n+1}\binom{2n}{n}$

which is the nth Catalan number.

Catalan numbers are the answers to a large number of questions. For example, C_n is also the number of ways to fully parenthesize a product of n + 1 terms, and the number of full binary trees with n + 1 nodes.

The Catalan numbers have been very well studied, and we know that asymptotically

$C \sim \frac{4^n}{n^{3/2} \sqrt{\pi}}$

so we can estimate C_n for large n. For example, we could use the formula above to estimate the number of ways to triangulate a 100-gon to be 5.84 ×10⁵⁵. The 98th Catalan number is closer to 5.77 ×10⁵⁵. Two takeaways: Catalan numbers grow very quickly, and we can estimate them within an order of magnitude using the asymptotic formula.

Equivalence classes

Now let’s go back and count the number of triangulations again, considering some variations on a triangulation to be the same triangulation.

We’ll consider rotations of the same triangulation to count only once. So, for example, we’ll say there is only one triangulation of a pentagon and four triangulations of a hexagon. If we consider mirror images to be the same triangulation, then there are three triangulations of a hexagon, counting the N pattern and the backward N pattern to be the same.

Grouping rotations

The number of equivalence classes of n-gon triangulations, grouping rotations together, is OEIS sequence A001683. Note that the sequence starts at 2.

OEIS gives a formula for this sequence:

$a(n) = \frac{1}{2n}C_{n-2} + \frac{1}{4}C_{n/2-1} + \frac{1}{2} C_{\lceil (n+1)/2\rceil - 2} + \frac{1}{3} C_{n/3 - 1}$
where C_x is zero when x is not an integer. So a(6) = 4, as expected.

Grouping rotations and reflections

The number of equivalence classes of n-gon triangulations, grouping rotations and reflections together, is OEIS sequence A000207. Note that the sequence starts at 3.

OEIS gives a formula for this sequence as well:

$a(n) = \frac{1}{2n}C_{n-2} + \frac{1}{4}C_{n/2-1} + \frac{1}{2} C_{\lceil (n+1)/2\rceil - 2} + \frac{1}{3} C_{n/3 - 1}$

As before, C_x is zero when x is not an integer. This gives a(6) = 3, as expected.

The formula on the OEIS page is a little confusing since it uses C(n) to denote C_n−2 .

[1] Our polygons do not need to be regular, but they do need to be convex.

How many ways can you triangulate a regular polygon?