Logarithmic sawtooth

Here’s a strange integral I ran across recently [1].

It’s a little surprising that the integral even exists, and more surprising that its value has a simple expression.

Here’s a plot of the integrand.

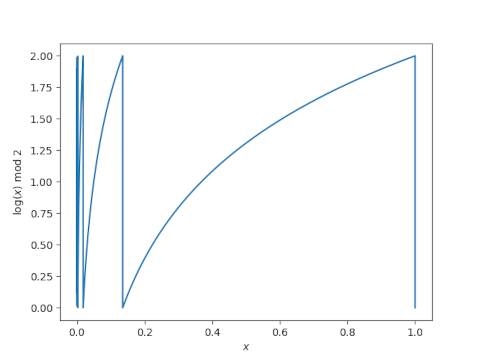
The plot doesn’t do justice to all the activity on the left end. There are an infinite number of increasingly vertical segments piled up on the left end as x goes to 0.

If you were to plot the integrand on a log scale, you’d get a sawtooth wave, stretching back to negative infinity.

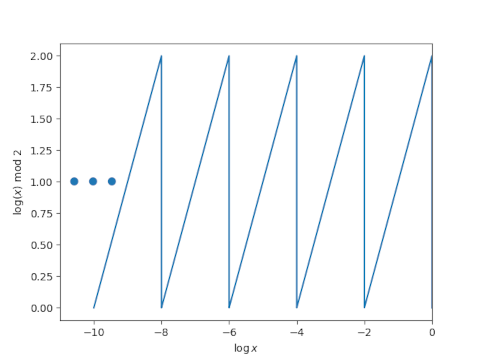
I would expect the integral to be difficult to evaluate numerically without some special handling, but SciPy’s quod function does a decent job by default.

    from numpy import log, tanh
    from scipy.integrate import quad

    print(quad(lambda x: log(x)%2, 0, 1))
    print(1/tanh(1))

This evaluates the integral as 1.313042… while the exact value is 1.313035…

To the integrator’s credit, it warns of difficulties before producing the result:

IntegrationWarning: The maximum number of subdivisions (50) has been achieved.

If increasing the limit yields no improvement it is advised to analyze the integrand in order to determine the difficulties. If the position of a local difficulty can be determined (singularity, discontinuity) one will probably gain from splitting up the interval and calling the integrator on the subranges. Perhaps a special-purpose integrator should be used.

Related posts

• Sawtooth and replicative functions
• Driving vibrations with sawtooth waves
• Square waves, triangular waves, and Fourier series

[1] Matthew A. Niemiro. The Natural Logarithm Modulo 2. The American Mathematical Monthly, Vol. 128, No. 2 (FEBRUARY 2021), p. 177.