If you see a light moving in the sky, how could you tell whether it’s an airplane or a satellite? If it is a satellite, could you tell how high of an orbit it’s in?
For an object in a circular orbit,
v² = μ/r
where r is the orbit radius and μ is the standard gravitational parameter. For a satellite orbiting the earth,
μ = 5.1658 × 1012 km³/hr².
The orbit radius r is the earth’s radius R plus the altitude a above the earth’s surface.
r = R + a
where the mean radius of the earth is R = 6,371 km.
Angular velocity is
v / r = √(μ/r³)
This velocity is relative to an observer hovering far above the earth. An observer on the surface of the earth would need to subtract the earth’s angular velocity to get the apparent velocity [1].
from numpy import pi, sqrt
def angular_v(altitude): # in radians/hour
R = 6371 # mean earth radius in km
r = altitude + R
mu = 5.1658e12 # km^3/hr^2
return sqrt(mu/r**3)
def apparent_angular_v(altitude):
earth_angular_v = 2*pi/(23 + 56/60 + 4/3600)
return angular_v(altitude) - earth_angular_v
Here’s a plot of apparent angular velocity for altitudes between 350 km (initial orbit of a Starlink satellite) and geostationary orbit (35,786 km).
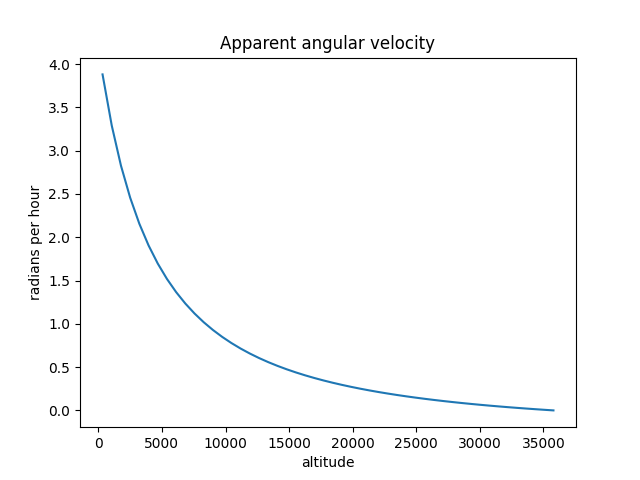
Radians per hour is a little hard to conceptualize; degrees per minute would be easier. But fortunately, the two are nearly the same. One radian per hour is 3/π = 0.955 degrees per minute.
The apparent size of the moon is about 0.5°, so you could estimate angular velocity by seeing how long it takes a satellite to cross the moon (or a region of space the width of the moon). It would only take an object in low earth orbit (LEO) a few seconds to cross the moon.
Can you see objects in medium earth orbit (MEO) or high earth orbit (HEO)? Yes. Although most satellites are in LEO, objects in higher orbits may be larger, and if they’re reflective enough they may be visible.
Airplanes move much slower than LEO satellites. An airliner at altitude 10 km moving 1000 km/hr would have an apparent angular velocity of 0.16 radians per hour. An object appearing to move that slowly is either an airplane or an object in HEO, and very likely the former.
[1] The earth completes a full rotation (2π radians) in 23 hours 56 minutes and 4 seconds, so its angular velocity is 0.2625 radians per hour. Why not 24 hours? That’s the length of a rotation of the earth relative to the sun. Since the earth moves in its orbit relative to the sun while it rotates, it has to rotate a little longer (i.e. for about 4 more minutes) to reach the same position relative to the sun.