Closed-form minimal surface solutions

Differential equations, especially nonlinear differential equations, rarely have a closed-form solution, but sometimes it happens. As I wrote about a year ago

It is unusual for a nonlinear PDE to have a closed-form solution, but it is not unheard of. There are numerous examples of nonlinear PDEs, equations with important physical applications, that have closed-form solutions.

This post will present some closed-form solutions of the minimal surface equation

(1 + |u_x|²) u_yy − 2 u_x u_y u_xy + (1 + |u_y|²) u_xx = 0

One trivial class of closed-form solutions are planes.

u(x, y) = ax + by + c.

There are three non-trivial classes of solutions as far as I know. Jean Baptiste Marie Meusnier discovered two of these in 1776, namely the helicoild

u(x, y) = tan⁻¹(y/x)

and the catenoid

u(x, y) = cosh⁻¹(a (x² + y²)^½) / a

Heinrich Scherk discovered another closed form solution in 1830:

u(x, y) = log( cos(ay) / cos(ax) ) / a

Here’s a plot.

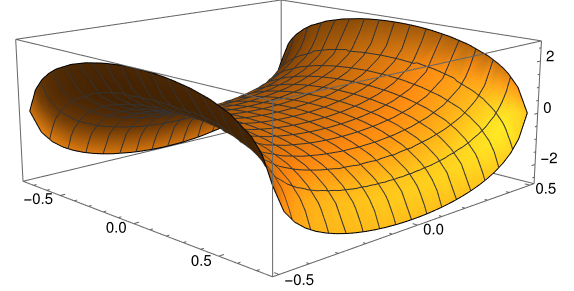
The surface formed by the graph of the solution is known as Scherk’s surface. You could image that if the edges of this surface were made of wire and the wire was dipped in soapy wanter, it would form a bubble like Sherk’s surface.

Note that the closed-form solutions satisfy the minimal surface PDE itself, but do not satisfy any given boundary conditions, unless the boundary values you’d like to specify happen to be exactly the values this function has.