An ellipse has equation
and a hyperbola has equation
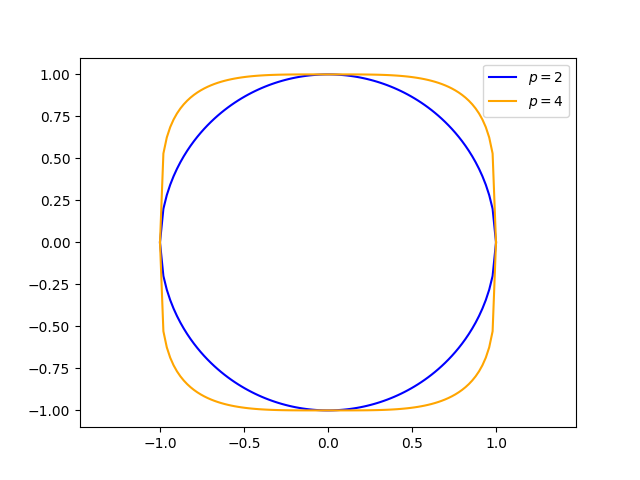
Similarly the superellipse has equation
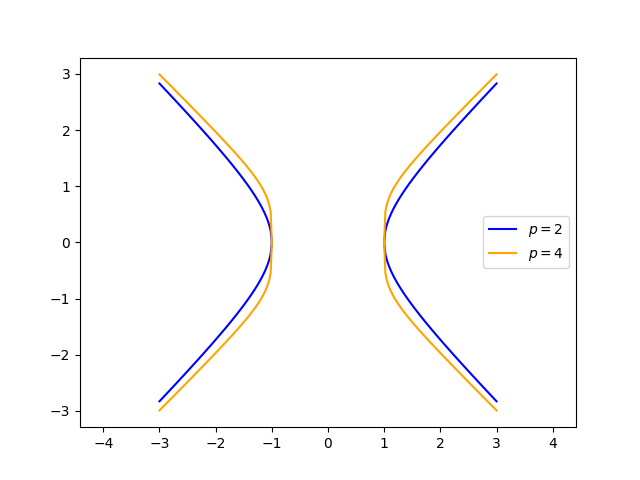
and the superhyperbola
When p = 2, the absolute value signs are unnecessary and the superellipse and superhyperbola reduce to the ellipse and hyperbola respectively.
Increasing p makes the superellipse more like a rectangle. But unlike a rectangle with rounded corners, the change in curvature is continuous.
Increasing p makes the superhyperbola more blunt at the vertices.
Marketing
The superellipse is a fairly well known variation on an ellipse. Even if you’re not familiar the term, you’ve probably seen the shape. I give a couple examples here. The superhyperbola is the obvious analog of a superellipse, but the term is far less common. I’d never hear the term until yesterday.
It’s not clear why the superellipse would be common and the superhyperbola obscure, but here’s some speculation. First of all, the superellipse had an advocate, Piet Hein. If the superhyperbola has an advocate, he’s not a very effective advocate.
The name is also off-putting: juxtaposing super and hyper sounds silly. The etymology makes sense, even if it sounds funny. Piet Hein used the prefix super– to refer to increasing the exponent from the usual value of 2. Its unfortunate that hyperbola begins with a root that is similar to super.

How about superbola?
Purely as a data point,
I will comment that independent of the merits of this post—which is lovely and interesting and I’m glad to have been directed to it—I did notice myself catching on the gendered _he_ in the comment about the superhypothetical proponent of the superhyperbola.
I’m old enough and male enough to still find singular “they” a bit awkward, but, it is interesting to see I have now fully internalized the expectation to see it.
Using “he” when the sex of a person is unknown was standard English grammar from the Anglo Saxon period until yesterday.
Superbola would be a catchy name
Thankfully a lot has changed since the Anglo Saxon period.
I remember your “squircle” post earlier and appreciate topics that combine mathematics and design.
The ellipse and hyperbola can be arranged into orthogonal families of curves. That is, for two given foci, all the ellipses that share those foci have perpendicular intersections with all hyperbolas of the same foci. (Hope I got this right; I read _Geometry and the Imagination_ so many years ago.)
Anyways, one has to wonder if super-ellipses and super-hyperbolas can also be arranged this way?
Have to give a nod to Piet Hein here, through whom I first encountered the superellipse. The super- prefix may be due to him as well.