The GELU (Gaussian Error Linear Units) activation function was proposed in [1]. This function is x Φ(x) where Φ is the CDF of a standard normal random variable. As you might guess, the motivation for the function involves probability. See [1] for details.
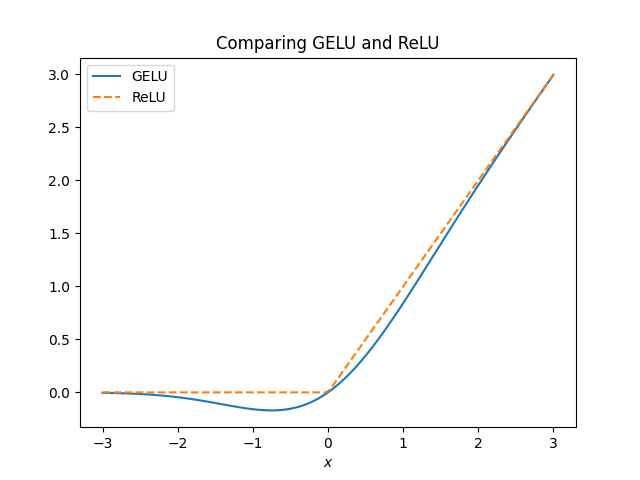
The GELU function is not too far from the more familiar ReLU, but it has advantages that we won’t get into here. In this post I wanted to look at approximations to the GELU function.
Since an implementation of Φ is not always available, the authors provide the following approximation:
I wrote about a similar but simpler approximation for Φ a while back, and multiplying by x gives the approximation
The approximation in [1] is more accurate, though the difference between the exact values of GELU(x) and those of the simpler approximation are hard to see in a plot.
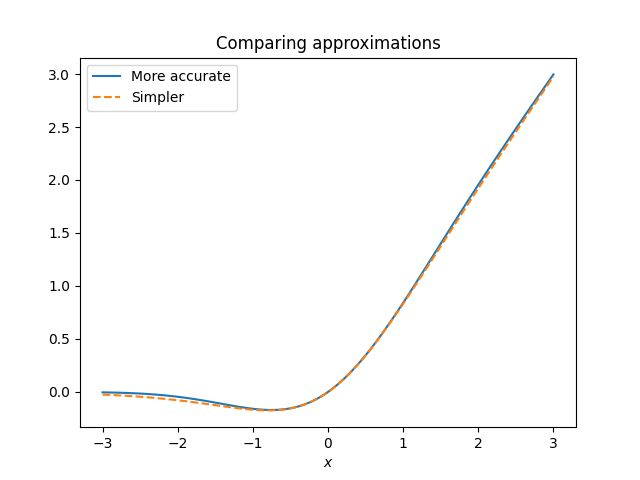
Since model weights are not usually needed to high precision, the simpler approximation may be indistinguishable in practice from the more accurate approximation.
Related posts
[1] Dan Hendrycks, Kevin Gimpel. Gaussian Error Linear Units (GELUs). Available on arXiv.
