A blog carnival is a way to discover new blogs. Writers on a given topic, such as math, take turns hosting the carnival, featuring recent posts from various writers. Blog carnivals were once much more common, but most have faded away.
The Carnival of Mathematics, however, is one of the oldest carnivals and still active, as evidenced by the fact that this is the 235th edition of the Carnival.
I’ve hosted the Carnival here several times. The first time was #50 and the most recent was #222.
The Aperiodical is a sort of meta-host for the Carnival: you can find past and future hosts by visiting this site.
Number trivia
It is traditional for the nth edition of the Carnival of Mathematics to begin with trivia about the number n.
According to Number Gossip, “235 is the smallest number whose first two digits are distinct primes such that their sum equals the third digit.”
235 is a centered triangular number. The figure below contains 235 dots.
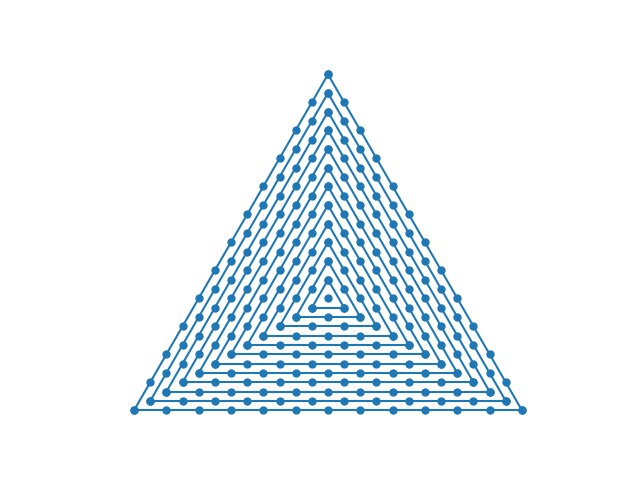
235 is a semiprime, i.e. the product of two prime numbers, in this case 5 and 47. There is a theorem that says there is only one group of order pq if p and q are prime, p > q, and q is not a factor of p − 1, and so there is only one group with 235 elements, namely the direct sum of the cyclic groups of order 5 and 47.
Post submissions
There were two links to Terence Tao‘s site this time. The first was an announcement for the AI for Math fund. The second was Tao’s brief notes on quaternions and spherical trigonometry.
We have a link from a post by Mike Croucher on solving higher-order ODEs in MATLAB. As with many software environments, MATLAB does not directly support higher-order ODEs but does support systems of first-order ODEs, and you can always convert the former to the latter. Croucher shows how to do this conversion, first by hand and then by using MATLAB’s symbolic calculation features.
Ionna Georgiu has posted a collection of videos on a variety of topics, including evidence of what we now call the Pythagorean theorem a millennium before Pythagoras.
Someone submitted to a Xena Project post by Kevin Buzzard on formalizing Fermat’s Last Theorem (FLT) in Lean. One line that struct me from the article was “We’re not formalising the old-fashioned 1990s proof of FLT. Since then, work of many people … led to the proof being generalised and simplified …” So in one generation, Wiles’ proof has gone from ground-breaking to old-fashioned.
Sophie Huiberts made a video entitled Open Problems and Diet Problems about linear programming, optimizing a linear objective function subject to linear constraints. The simplex method for solving such optimization problems performs much better in practice than in worst-case theory. In practice the time required to execute the algorithm is proportional to the size of the problem, but one can construct artificial problems for which the time required grows exponentially with the problem size. Huiberts looks at a probabilistic explanation of why the simplex method works so well, but concludes that the explanation is not satisfying.
