Here’s a visualization of how the day of the week for New Year’s Day changes.
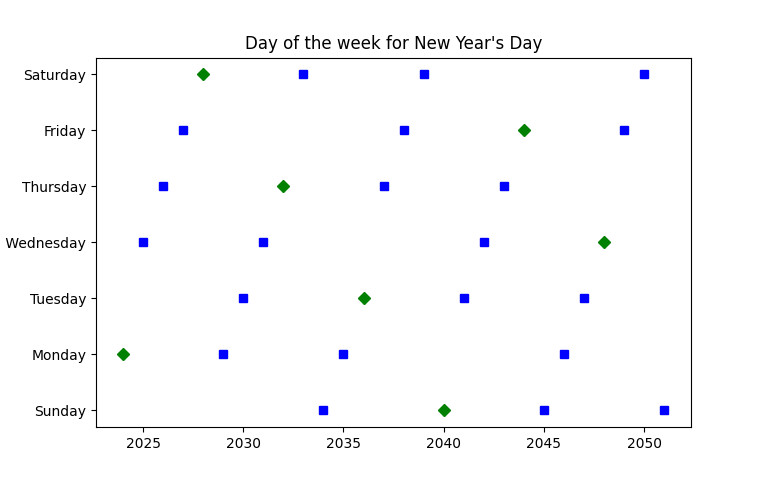
The green diamonds represent leap years and the blue squares represent ordinary years.
The day of the week for New Year’s Day advances one day after each ordinary year and two days after each leap year, hence the diagonal stripes in the graph above.
The whole cycle repeats every 28 years. During that 28 year cycle, New Year’s Day falls on each day of the week four times: three times in an ordinary year and once in a leap year. Or to put it another way, each horizontal row of the graph above contains three blue squares and one green diamond.
The comments above are true under the Julian calendar, without exception. And they’re true for long stretches of time under the Gregorian calendar. For example, the pattern above repeats from 1901 to 2099.
The Julian calendar had a leap day every four years, period. This made the calendar year longer than the solar year by about 3 days every 400 years, so the Gregorian calendar removed 3 leap days. A year divisible by 100 is not a leap year unless it is also divisible by 400. So the Gregorian calendar disrupts the pattern above every 100 years.
