No matter what number you start with, if you press the cos key on a calculator repeatedly, the numbers eventually quit changing. This fact has been rediscovered by countless children playing with calculators.
If you start with 0, which is likely the default when you turn on a calculator, you’ll hit the final value after 90 steps [1]. You could verify this with the following Python code.
from math import cos
x = 0
for i in range(100):
x = cos(x)
print(i, x)
Starting with iteration 90, the code prints 0.7390851332151607 every time.
Visualizing convergence
Let’s visualize the sequence of values using a cobweb plot. Here’s an image I made for a post four years ago, starting with x = 1.
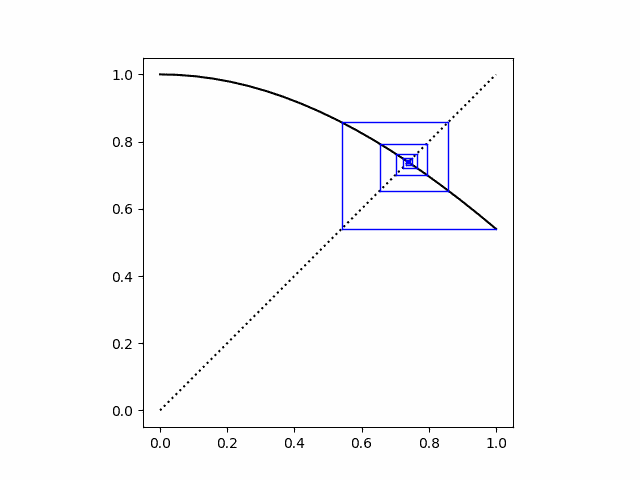
To read the graph, start at x = 1 on the horizontal axis. The solid black line is a plot of the cosine function, and so the point above 1 where the blue line starts is y = cos(1) = 0.54.
Since we’re going to stick our output back into cosine as input, we need to turn our y into an x. We do this by sliding the point over to the dotted line representing y = x. This creates the horizontal blue line that is the first segment of our spiral. This takes us to the point (cos(1), cos(1)).
Now when we take the cosine again, we get cos(cos(1)) = 0.86. Now we move from our previous value of y = 0.54 to our new value of y = 0.86. This gives the next segment of our spiral. Again we need to turn our y into an x, so we slide over to the line y = x as before, only this time we’re approaching from the left side rather than from the right.
We quickly get to where we can no longer see the convergence. The plot above used 20 iterations, and we end up with a blue blob around the point of convergence.
Proving convergence
We said that the iteration converges for any starting point. Why is that?
For one thing, we might as well assume x is between 0 and 1; if not, it will be after one iteration.
The mean value theorem says for any pair x1 and x2 in [0, 1],
cos(x1) − cos(x2) = − sin(c) (x1 − x2)
for some c in [0, 1] because the derivative of cos(x) is − sin(x). It follows that
| cos(x1) − cos(x2) | ≤ sin(1) | x1 − x2 |
because the maximum value of sin(x) on [0, 1] is sin(1). Since sin(1) = 0.84… is less than 1, this says that cosine is a contraction mapping on [0, 1] and so there is a fixed point p such that cos(p) = p.
Rate of convergence
We could use this to calculate an upper bound on how far x is from the fixed point p after k iterations:
| x − p | ≤ sin(1)k
and so if we want to be within a distance ε of the fixed point, we need
k ≥ log(ε) / log(sin(1)).
This says that to get withing floating point precision (about 10−16) of the fixed point, 214 iterations will do. This is true, but it’s a pessimistic estimate because it’s based on a pessimistic estimate of sin(c).
Once we get close to the fixed point p, the rate of convergence is more like sin(p)k than sin(1)k. This suggests we should be within floating point precision of the fixed point after about 90 iterations, which is what we saw at the top of the post.
More fixed point posts
- Kepler and the contraction mapping theorem
- Lagrange points
- Normal probability fixed point
- Möbius transformation fixed points
- Fourier transform fixed points
[1] This is true if your calculator is using 64-bit floating point numbers. Your mileage may vary if you have a calculator that retains more or less precision.
