Binomial bound

I recently came across an upper bound I hadn’t seen before [1]. Given a binomial coefficient C(r, k), let

n = min(k, r − k)

and

m = r −  n.

Then for any ε > 0,

C(n + m, n) ≤ (1 + ε)^{n + m} / εⁿ.

The proof follows quickly from applying the binomial theorem to (1 + ε)^{n + m}.

I could imagine how non-optimal choice of ε could be convenient in some context, it’s natural to want to see how good the upper bound is for the best ε, which works out to be ε = n/m.

A little algebra shows this value of ε leads to

C(n + m, n) ≤ (n + m)^{n + m} / nⁿ m^m.

Note that while the original bound is not symmetric in n and m, the optimal bound is.

Returning to the original notation C(r, k), let’s see how tight the optimal bound is by plotting, as a function of r, the maximum relative error as a k varies.

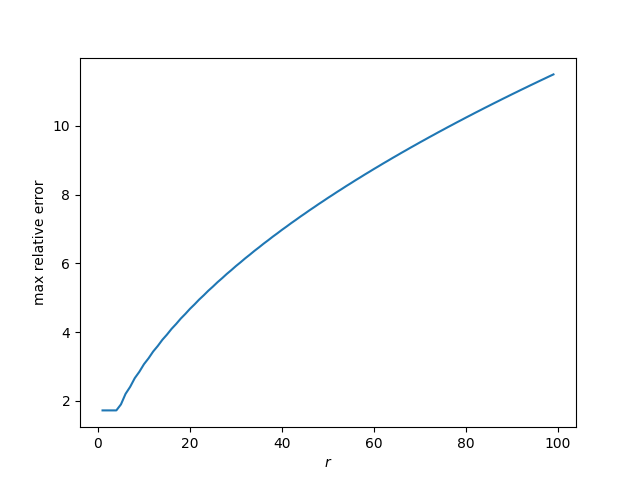
The maximum relative error, over the range plotted, is very roughly r/10.

Related posts

• Bounds on the central binomial coefficient
• Non-integer binomial coefficients
• q-binomial coefficients

[1] Grzegorz Łysik. The ε-binomial inequality. The Mathematical Gazette. Vol. 92, No. 523 (March 2008), pp. 97–99