Normal approximation to normal

In my previous post on approximating a logistic distribution with a normal distribution I accidentally said something about approximating a normal with a normal.

Obviously the best approximation to a probability distribution is itself. As Norbert Wiener said “The best material model of a cat is another, or preferably the same, cat.”

But this made me think of the following problem. Let f be the density function of a standard normal random variable, i.e. one with mean zero and standard deviation 1. Let g be the density function of a normal random variable with mean μ > 0 and standard deviation σ.

For what value of σ does g best approximate f? Is it simply σ = 1? Does it depend on μ?

I looked at the 1, 2, and ∞ norms, and in each case the optimal value of σ is not 1, and the optimal value does depend on μ. When μ is close to 0, σ is close to 1, as you’d probably expect. But for larger μ the results are surprising.

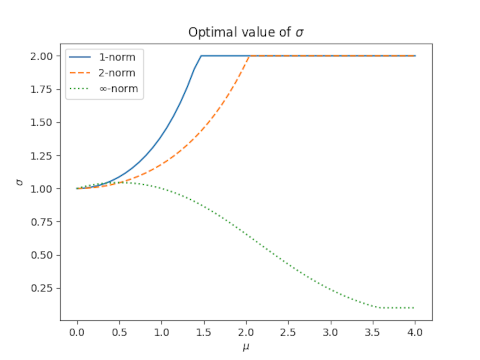
For the 1-norm and 2-norm, the optimal value of σ increases with μ and reaches a maximum of 2, then remains constant.

For the ∞ norm, the optimal value of σ increases briefly then decreases.