Zeta sum vs zeta product

Posted on by John

The Riemann zeta function ζ(s) is given by an infinite sum and an infinite product

\zeta(s) = \sum_{n=1}^\infty\frac{1}{n^s} = \prod_{p \text{ prime}} \frac{1}{1-p^{-s}}

for complex numbers s with real part greater than 1 [*].

The infinite sum is equal to the infinite product, but which would give you more accuracy: N terms of the sum or N terms of the product? We’ll take a look at this question empirically.

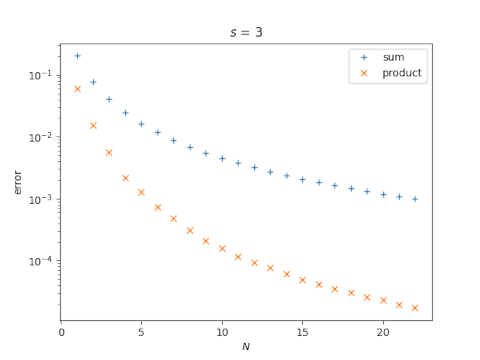
The accuracy of the partial sum and the partial product depends on N and on s. For starters, let’s fix s = 3 and look at the approximation error as a function of N. Note that the error is plotted on a log scale.

Now let’s fix N = 10 and look at the error as a function of s.

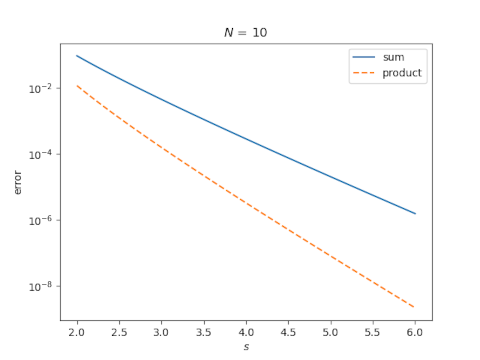
So our two examples suggest that taking N terms of the product gives more accuracy than taking N terms of the sum.

In the paper mentioned in the previous post, the author approximates the zeta function with a few terms of the product. That’s what motivated this post. I thought the product might give more accuracy than the sum, and that appears to be the case.

Related posts

[*] If you evaluate the series for ζ at s = -1, despite the fact that the equation does not hold at that point, and evaluate ζ at -1 using analytic continuation, you get the infamous nonsensical result that the positive integers sum to -1/12.

2 thoughts on “Zeta sum vs zeta product”

  1. GlennF

    It’s not too surprising… Even at N = 1, the product is winning because it corresponds to the sum over all multiples of 2, not just the single ‘2’.
    Similarly N =2 contains all multiples of 2 and 3 (2^i * 2^j), etc.

Comments are closed.