Douglas Hofstadter, best known as the author of Godel, Escher, Bach, wrote the foreword to Clark Kimberling’s book Triangle Centers and Central Triangles. Hofstadter begins by saying that in his study of math he “sadly managed to sidestep virtually all of geometry” and developed an interest in geometry, specifically triangle centers, much later.
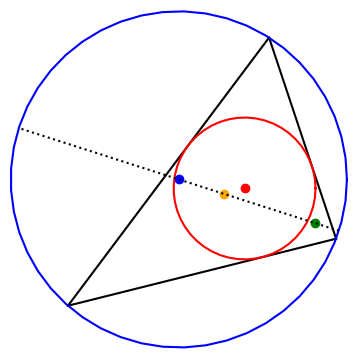
The ancient Greeks had four ways to define the center of a triangle—circumcenter, incenter, orthocenter, and centroid. These are marked in the diagram above in blue, red, green, and orange respectively. But there are many more notions of a center of a triangle. Kimberling’s book (published in 1998) gives 400 triangle centers, and his website now lists tens of thousands of triangle centers.
In the foreword to Kimberling’s book Hofstadter recounts his speculation regarding which notion of triangle center is most central, the most important. He debates several criteria, then focuses on the fact that triangle centers tend to lie on lines, like the Euler line drawn in the image above. He calculates that the first 100 centers on Kimberling’s list fall on far fewer lines than one would expect if the points were distributed randomly.
So one could rank the lines according to how many centers each had, and rank the centers by how many lines pass through each. But then you want to count the ranks of the lines, giving points a higher rank for being on more high ranking lines, and you want rank lines higher for having more high ranking points on them ….
Hofstadter says that although this sounds circular, and it is, his ranking system could be implemented as a system of linear equations.
This system for ranking triangle centers is essentially the same as Google’s PageRank algorithm, giving higher rank to pages that are linked to by high ranking pages. And computing PageRank is indeed an enormous linear algebra problem, specifically an eigenvalue problem.
Hofstadter was not the first to think of this kind of ranking. According to Wikipedia
The eigenvalue problem behind PageRank’s algorithm was independently rediscovered and reused in many scoring problems. In 1895, Edmund Landau suggested using it for determining the winner of a chess tournament.
Hofstadter says
It would be fascinating to see what would come out of this attempt to assign a rank-ordering to the special points and special lines associated with any triangle.
But apparently he did not carry out the calculation, at least not as of 1998. Perhaps the idea of solving an eigenvalue problem for a matrix with hundreds of rows seemed impractical to Hofstadter at the time.
It would be interesting to know whether Hofstadter or anyone else ever followed through on this ranking project.
Kimberling lists his triangle centers in roughly chronological order, which correlates with subjective importance. If someone were to carry out a PageRank of the triangle centers, I’d recommend using only the 400 centers in Kimberling’s book. Or maybe even better, repeat the exercise for the first N centers for an increasing sequence of values of N.

I think a more catchy title to this post (say, “What’s the most central center of a triangle?”) might have attracted people to actually try out carrying the calculation :)
“He calculates that the first 100 centers on Kimberling’s list fall on far fewer lines than one would expect if the points were distributed randomly.”
Thus seems completely counterintuitive.
If by “randomly” he means from a 2D uniform distribution over the area of the triangle and some of its surrounding neighborhood, I would expect three collinear points to occur from a finite sample of points with probability zero.
I must be missing something.