Evolute of an ellipse

Suppose you’re standing on an ellipse. (You actually are: lines of longitude are elliptical because of earth’s equatorial bulge.)

Now draw a line perpendicular to where you’re standing. Lines of longitude are nearly circles, but we’ll look at a more obviously elliptical ellipse.

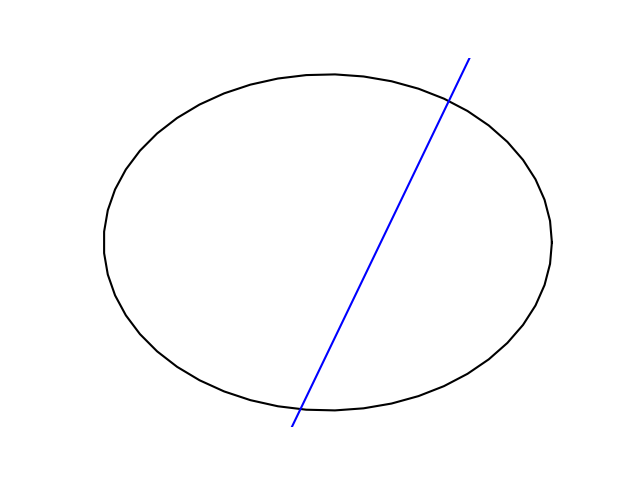
The line is perpendicular to the northeast side of the ellipse where it starts, but not where it crosses on the other side.

Now suppose lots of people standing on the circle all draw perpendicular lines. We get a surprising result.

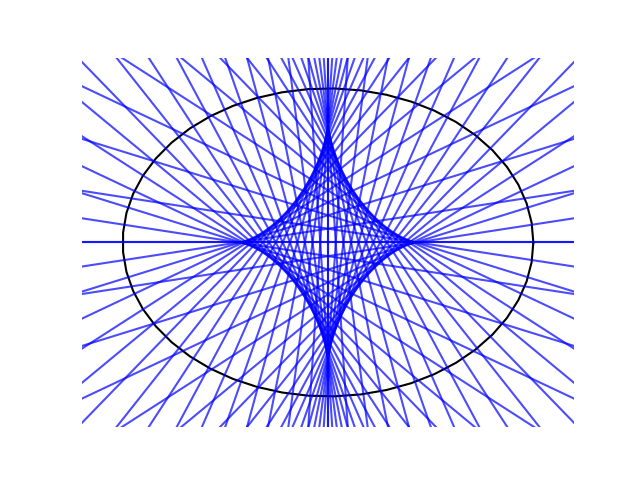
If we did this with a circle, all we’d see is lines radiating out of the center of the circle. But for an ellipse we get something much more interesting.

There’s a simple equation for the star-like figure in the middle created by all the normal lines. We’ll get to that shortly, but first we need to talk about kissing circles.

Kissing circles

Suppose you wanted to approximate an ellipse by pieces of a circle, as is sometimes done in computer graphics. What radius should you use?

The circle that best approximates a curve at a point is called the kissing circle, or classically the osculating circle. The radius of this circle is the radius of curvature at the point where it touches the curve.

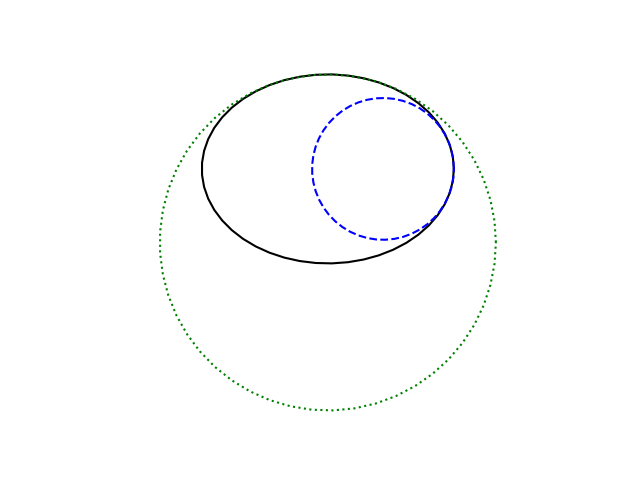
In the image above, the small blue circle is the best approximation of the ellipse on the side. The much bigger green circle is the best approximation to the ellipse on the top. The centers of these two circles are the centers of curvature at the two points on the curve.

Equation of evolute

We could visualize all centers of curvature by plotting the center of curvature for each point on the curve. This is called the evolute of the curve.

If we parameterize our ellipse by

x(t) = a cos t
y(t) = b sin t

then the evolute has parameterization

x(t) = (a² – b²) cos³ t / a
y(t) = (b² – a²) sin³ t / b

You can find a general formula for the evolute to any parameterized curve in the next post.

Here’s what it looks like.

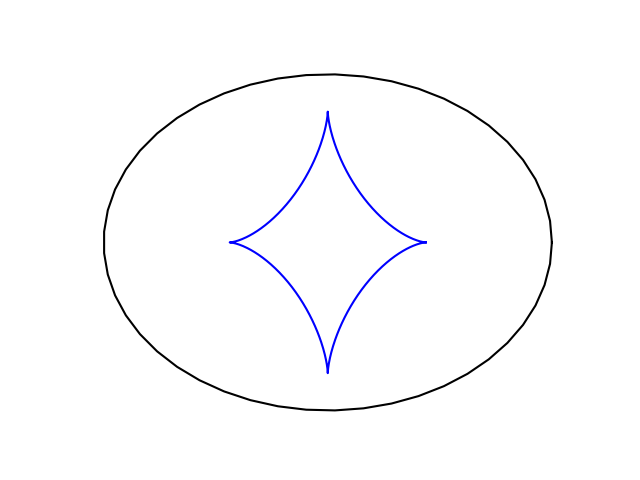
This is the same shape as the figure formed by the normal lines at the top of the post. The lines that are normal to the ellipse are tangent to its evolute. To confirm this, we’ll plot the normal lines again and plot the evolute on top in red.

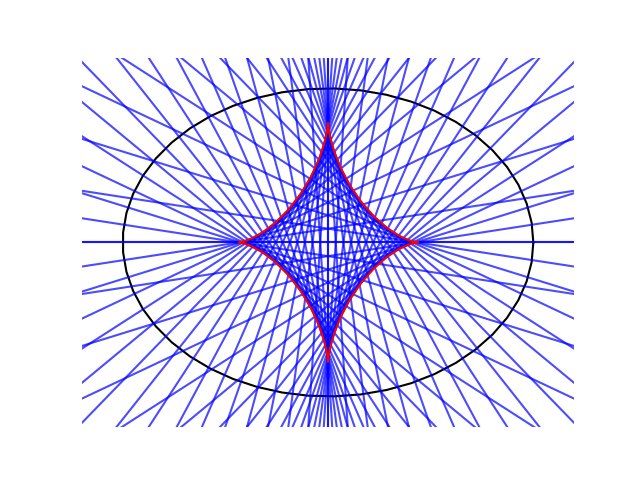
Incidentally, the evolute of an ellipse can extend outside the ellipse, and it will if the ellipse is more eccentric. Here’s an example.

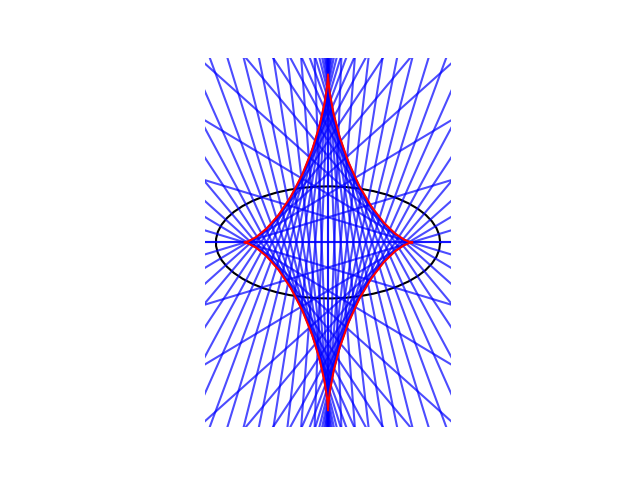
The next post looks at a curve whose evolute is another curve of the same kind.

Similar posts

• Evolute of an egg
• Envelopes of epicycloids