Blaschke factors

Blaschke factors are complex functions with specified zeros inside the unit disk. Given a complex number a with |a| < 1, the Blaschke factor associated with a is the function

Notice the semicolon in b(z; a). This is a convention that a few authors follow, and that I wish more would adopt. From a purely logical perspective the semicolon serves no purpose because the expression on the right is a function of two variables, z and a. But the semicolon conveys how we think about the function: we think of it as a function of z that depends on a parameter a.

So, for example, if we were to speak of the derivative of b, we would mean the derivative with respect to z. And we could say that that b is an analytic function inside the unit disk. It is not an analytic function if we think of it as a function of a because of taking the conjugate of a in the denominator.

The function b(z; a) has a zero at a and a pole at the reciprocal of the conjugate of a. So, as I wrote about yesterday, this means that the zero and the pole are inversions of each other in the unit circle. If you punch a hole in the complex plane at the origin and turn the plane inside-out, without moving the unit circle, the zero and pole will swap places.

Here’s a plot of b(z; 0.3 + 0.3i).

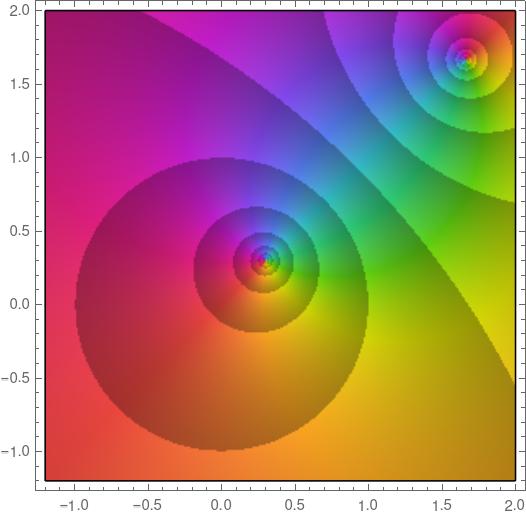
Notice there’s a zero at 0.3 + 0.3i and a pole at

1/(0.3 – 0.3i) = 5/3 + 5/3i

which is the inversion of 0.3 + 0.3i in the unit circle. You can tell that one is a zero and the other is a pole because the colors rotate in opposite directions.

The plot above was made with the following Mathematica code.

    b[z_, a_] := (Abs[a]/a) (a - z)/(1 - Conjugate[a] z)
    ComplexPlot[b[z, .3 + .3 I], {z, -1.2 - 1.2 I, 2 + 2 I}, 
        ColorFunction -> "CyclicLogAbs"]

Because the zero and pole locations are inversions of each other, as the zero moves closer to the unit circle from the inside, the pole moves closer to the unit circle from the outside. Here’s a plot with a = 0.5 + 0.5i.

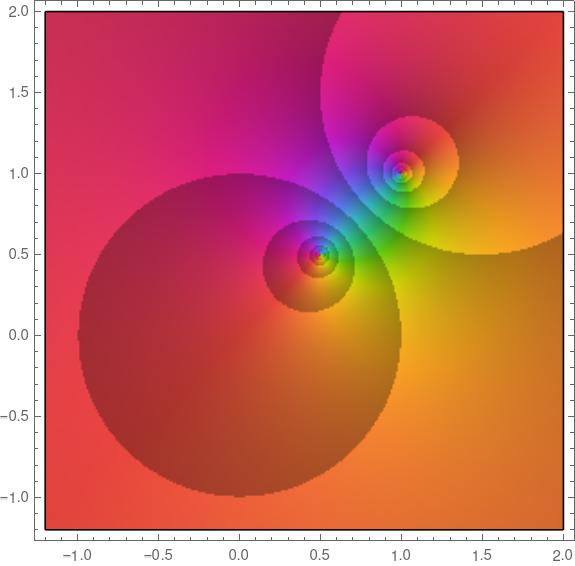
And the closer the zero gets to the origin, the further out the pole moves. Here’s a plot with a = 0.2 + 0.2i, this time on a larger scale, this time with the real and imaginary axes going up to 3 rather than 2.

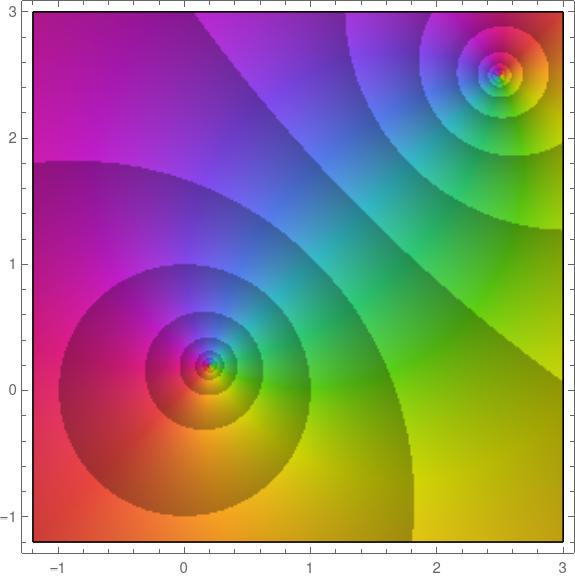
Blaschke factors are the building blocks of Blaschke products, something I intend to write about in the future. By multiplying Blaschke factors together, you can create function that is analytic in the unit disk with specified zeros and with other nice properties.

Elias Wegert [1] says “In some sense, Blaschke products can be considered to be ‘hyperbolic counterparts’ of polynomials.” That’s something I’d like to explore further.

Related posts

• Inversion in a circle
• Conformally mapping Mickey Mouse into Batman

[1] Elias Wegert. Visual Complex Functions: An Introduction with Phase Portraits. Birkhäuser.