Partitions of unity are a handy technical device. They’re seldom the focus of attention but rather are buried in the middle of proofs.
The name sounds odd, but it’s descriptive. A partition of unity is a set of smooth functions into the interval [0, 1] that add up to 1 at every point. The functions split up (partition) the number 1 (unity) at each point. The functions are chosen to have properties that let you glue together local results to create a global result.
Smooth ramp functions
Proving the existence of partitions of unity with the desired properties isn’t trivial. One of the steps along the way is to prove that you can create functions than ramp up smoothly between constant values. You want to show there are functions f that equal 0 on one side of a closed interval [a, b] and equal 1 on the other side. That is, you can choose f such that f(x) = 0 for x ≤ a and f(x) = 1 for x ≥ b. You can also require f to be monotone increasing over the interval [a, b].
It may seem obvious that smooth ramp functions exist, but they do not exist if you require your functions to have a power series at every point. Ramp functions can be infinitely differentiable, but they cannot be analytic.
Smooth ramp functions are used everywhere, but they’re complicated to write down explicitly.
CW clicks
Morse code is sent over a radio using CW, continuous wave. The name is historical, contrasting with an early method known as damped wave.
To send a dot or a dash, you send a short or a long pulse of a fixed pitch. If you abruptly turn this tone on and off you’ll create noisy side effects called clicks. As I wrote about in this post, an abrupt change in frequency creates broad spectrum side effects, but smoothing the transition greatly reduces the bandwidth.
The recommended rise and fall time for a CW pulse is between 2 and 4 milliseconds. So if a dot is transmitted as a 50 ms pulse, your equipment might shape the pulse to be a 42 ms pulse at full amplitude with 4 ms transitions on each side where the amplitude smoothly rises and falls. That is, you multiply your pulse by a couple of smooth ramp functions as described above.
Here’s a plot for a pulse of a 800 Hz tone.
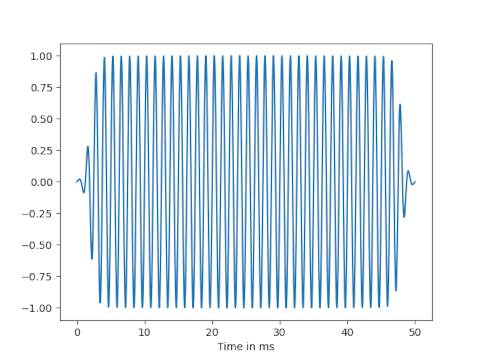
This minor modification of pulses makes no audible difference to the desired signal but greatly reduces unwanted effects.

One idea I’ve been toying with is to not apodize the pulses but to construct more or less ideal bandlimited rectangular pulse waves to begin with. This is a problem solved in the audio DSP literature by summing bandlimited impulse functions, read out of a wavetable, and then integrating/summing. The solution is used in the so called virtual analog (subtractive) synthesizers, in order to generate the analog basis waveforms in a modulable and strictly bandlimited form.
Of course such a solution loses the constant envelope properties of the conventional Morse code, requires a linear SSB tranceiver and DSP power, and might in fact be less intelligible than the standard solution which retains some wideband clicking. But the remarkable thing is that it can be done almost exactly, on the fly, with arbitrary timing, and if you use minimum phase signals, causally and with provably minimal keying delay. The resulting spectral efficiency ought to be even better than that of straight CW, especially when going HST, and the bandwidth can be exactly controlled simply by changing the bandwidth of impulses in the wavetable.