Multiplication theorem rabbit hole

Posted on by John

When I started blogging I was reluctant to allow comments. It seems this would open the door to a flood of spam. Indeed it does, but nearly all of it can be filtered out automatically.

The comments that aren’t spam have generally been high quality. A comment on my post about the sawtooth function a few days ago has sent me down a fascinating rabbit hole.The sawtooth function belongs to a general class of functions called replicative functions, functions that satisfy the equation

f(nx) = \sum_{i=0}^{n-1} f\left(x + \frac{i}{n} \right )

for positive integers n.

I ran across this by reading Knuth’s TAOCP. Knuth gives an understated comment in section 1.2.4 exercise 40 that “it may be interesting to study also the more general class of functions” for which the left-hand side above includes constants that depend on n, i.e.

a_n f(nx) + b_n = \sum_{i=0}^{n-1} f\left(x + \frac{i}{n} \right )

where the constants an and bn depend on n but not on x.

Bernoulli polynomials

The first Bernoulli polynomial B1(x) = x – ½ is a replicative function, and the only continuous replicative functions are multiples of B1 (proved in exercise 40 referenced above).

The rest of the Bernoulli polynomials Bm(x) are generalized replicative functions, with an = nm-1 and bn = 0. This was discovered by Joseph Raabe in the nineteenth century.

Gamma and digamma functions

Gauss’s multiplication theorem for the gamma function says that for positive n,

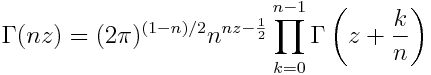
This is equation 6.1.20 in A&S. If we take logs of both sides, we find that log Γ is a almost a generalized replicative function.

\log \Gamma(nz) = \frac{1-n}{2}\log(2\pi) + \left(nz - \frac{1}{2}\right)\log n + \sum_{k=0}^{n-1} \log \Gamma\left(z + \frac{k}{n} \right )

The factor of n log(n) z prevents the definition from holding, but if we take derivatives, this term goes away.

This means that the derivative of log Γ, a.k.a the ψ function, a.k.a. the digamma function, is a generalized replicative function with an = n and bn = –n log n.

The derivative of a generalized replicative function is another function in the same class, so the higher derivatives of log Γ, known as the polygamma functions, are also generalized replicative functions.

Hurwitz zeta function

The Hurwitz zeta function ζ(s, z) is defined by

\zeta(s, z) = \sum_{k=0}^\infty \frac{1}{(z+k)^s}

The Riemann zeta function is the special case of the Hurwitz zeta function with z = 1.

The Hurwitz zeta function is related to the polygamma functions by

\psi^{(m)}(z)= (-1)^{m+1} m! \zeta (m+1,z)

It follows from this that for fixed s, ζ(s, z) is a generalized replicative function of z. You can show that an = ns and bn = 0.

Trig functions

See the next post for a couple examples involving trig functions: cot πx and csc² πx .

Related posts

One thought on “Multiplication theorem rabbit hole”

  1. There is an interesting extension of this whereby an integer multiple m is applied such that the sum runs over m*i/n and the left hand side becomes a function of the gcd(n, m). It means any replicative function can actually be used as an explicit means of calculating the gcd.

Comments are closed.