Plotting the Gauss map

Posted on by John

A recent post looked at an example from one of Michael Trott’s tomes. This post looks at another example from the same tome.

Trott made a contour plot of the Gauss map

f(x) = \frac{1}{x} - \left\lfloor \frac{1}{x}\right\rfloor

over the complex plane. I copied his code (almost) and reproduced his plot.

    ContourPlot[
        Abs[1/(x + I y) - Floor[1/(x + I y)]], 
        {x, -1.1, 1.1}, {y, -1.1, 1.1}, 
        PlotPoints -> 40, ColorFunction -> Hue, 
        ContourStyle -> {Thickness[0.00001]}
    ]

This produced the following image.

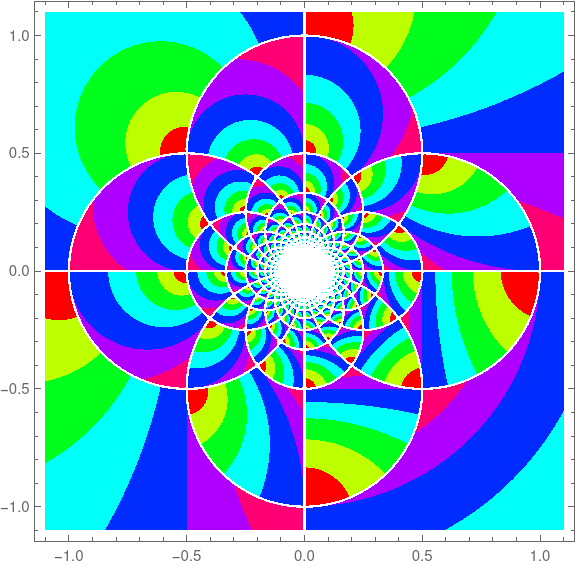
The original code set PlotPoints to 400, and it was taking forever. I got impatient and set the parameter to 40. Looking at the image in the book, it seems the plot with the parameter set to 400 is very similar, except there’s a black tangle in the middle rather than a white space.

In 2004 when Trott wrote his book, Mathematica did not have a command for plotting functions of a complex variable directly, and so Trott rolled his own as a function of two real variables.

Here’s a plot of the same function using the relatively new ComplexPlot function.

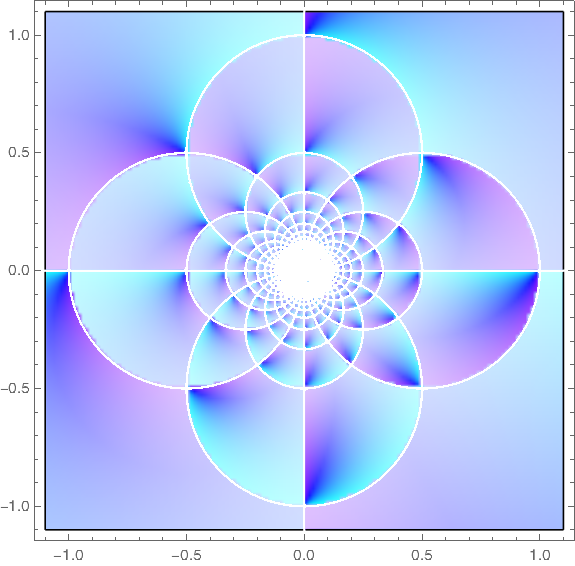
Here’s the code that produced the plot.

    ComplexPlot[
        (1/z - Floor[1/z]), 
        {z, -1.1 - 1.1 I, 1.1 + 1.1 I}, 
        ColorFunction -> Hue, PlotPoints -> 400
    ]

Update

What does it mean to apply the floor function to a complex number? See the next post.

The plots above were based on Mathematica’s definition of complex floor. Another definition gives different plots.

    aplfloor[z_] := 
        With[ {x = Re[z] - Floor[Re[z]], y = Im[z] - Floor[Im[z]], g = Floor[z]}, 
        If[x + y > 1, If[x >= y, g + 1, g + I], g]]

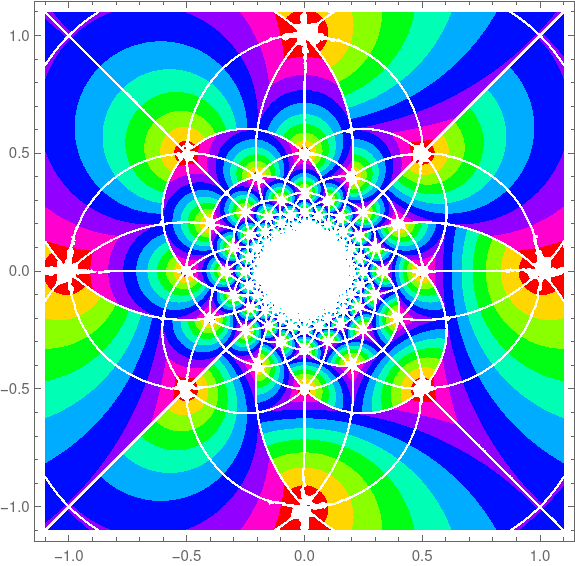
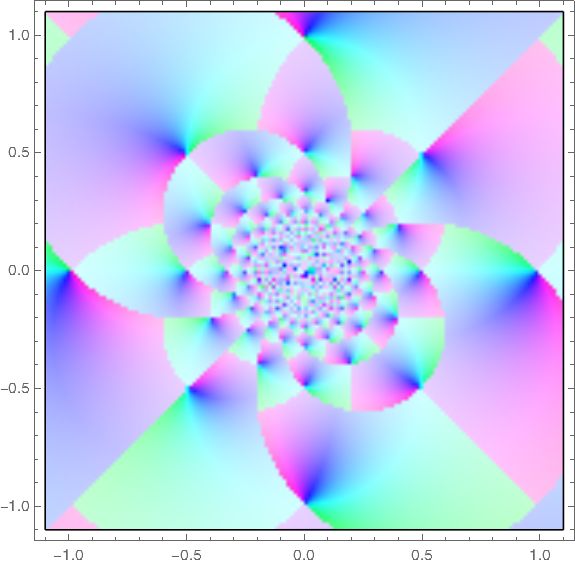
This leads to different plots of the Gauss map.

Vintage:

And new style:

Related posts

4 thoughts on “Plotting the Gauss map”

  1. Mildred Bonk

    I’m familiar with floor over the reals, but not over the complex numbers. How is it defined there?

  2. John

    Good question. Mathematica defines the floor of a complex number by taking the floor of the real and imaginary parts separately. That is, for real a and b, Mathematica defines Floor[a + bi] as Floor[a] + i Floor[b]. I don’t know whether any other source defines floor of a complex number that way, or defines it at all.

    [Update: I expanded this answer into the next post. A surprising bonus is that exploring the definition of floor for complex numbers lead to creating an interesting image.]

Comments are closed.