Superfactorial

The factorial of a positive integer n is the product of the numbers from 1 up to and including n:

n! = 1 × 2 × 3 × … × n.

The superfactorial of n is the product of the factorials of the numbers from 1 up to and including n:

S(n) = 1! × 2! × 3! × … × n!.

For example,

S(5) = 1! 2! 3! 4! 5! = 1 × 2 × 6 × 24 × 120 = 34560.

Here are three examples of where superfactorial pops up.

Vandermonde determinant

If V is the n by n matrix whose ij entry is i^j−1 then its determinant is S(n − 1). For instance,

$\begin{vmatrix} 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 8 \\ 1 & 3 & 9 & 27 \\ 1 & 4 & 16& 64 \end{vmatrix} = S(3) = 3!\, 2!\, 1! = 12$

V is an example of a Vandermonde matrix.

The number of Latin squares of size n is bounded below by S(n). More on Latin squares and upper and lower bounds on how many there are here.

One way to define the permutation symbol uses superfactorial:

$\epsilon_{i_1 i_2 \cdots i_n} = \frac{1}{S(n-1)} \prod_{1 \leq k < j \leq n} (i_j - i_k)$

The Barnes G-function extends superfactorial to the complex plane analogously to how the gamma function extends factorial. For positive integers n,

$G(n) = \prod_{k=1}^{n-1}\Gamma(k) = S(n-2)$

Here’s plot of G(x)

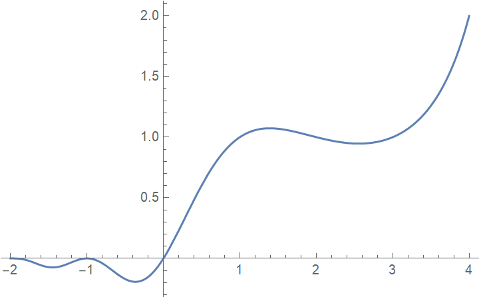
produced by

    Plot[BarnesG[x], {x, -2, 4}]

in Mathematica.

Aaron Meurer

15 September 2020 at 15:12

Your definition for G(n) seems to only be defined when n is a positive integer.
John

15 September 2020 at 15:20

The identity for G above is only valid for positive integers. It’s not a definition. There is a closed-form definition of G. It’s a little complicated, but if I remember correctly it just involves gamma, psi (derivative of log gamma), and exp.

Comments are closed.