A tale of two iterations

I recently stumbled on a paper [1] that looks at a cubic equation that comes out of a problem in orbital mechanics:

σx³ = (1 + x)²

Much of the paper is about the derivation of the equation, but here I’d like to focus on a small part of the paper where the author looks at two ways to go about solving this equation by looking for a fixed point.

If you wanted to isolate x on the left side, you could divide by σ and get

x = ((x + 1)² / σ)^1/3.

If you work in the opposite direction, you could start by taking the square root of both sides and get

x = √(σx³) − 1.

Both suggest starting with some guess at x and iterating. There is a unique solution for any σ > 4 and so for our example we’ll fix σ = 5.

We define two functions to iterate, one for each approach above.

    sigma = 5
    x0 = 0.1

    def f1(x):
        return sigma**(-1/3)*(x+1)**(2/3)

    def f2(x):
        return (sigma*x**3)*0.5 - 1

Here’s what we get when we use the cobweb plot code from another post.

    cobweb(f1, x0, 10, "ccube1.png", 0, 1.2)

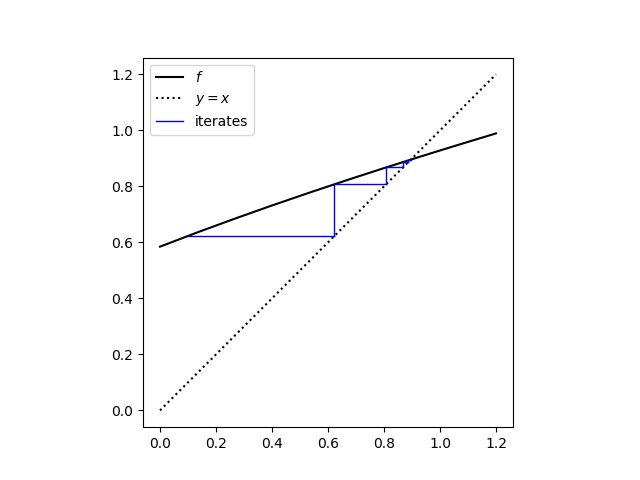
This shows that iterations converge quickly to the solution x = 0.89578.

Now let’s try the same thing for f2. When we run

    cobweb(f2, x0, 10, "ccube2.png", 0, 1.2)

we get an error message

    OverflowError: (34, 'Result too large')

Let’s print out a few values to see what’s going on.

    x = 0.1
    for _ in range(10):
        x = f2(x)
        print(x)

This produces

    -0.9975
    -3.4812968359375005
    -106.4783129145318
    -3018030.585561691
    -6.87243939752166e+19
    -8.114705541507359e+59
    -1.3358518746543001e+180

before aborting with an overflow error. Well, that escalated quickly.

The first iteration converges to the solution for any initial starting point in (0, 1). But the solution is a point of repulsion for the second iteration.

If we started exactly on the solution, the unstable iteration wouldn’t move. But if we start as close to the solution as a computer can represent, the iterations still diverge quickly. When I changed the starting point to 0.895781791526322, the correct root to full floating point precision, the script crashed with an overflow error after 9 iterations.

More on fixed points

• Kepler’s equation
• Contractions and weak contractions
• Fixed point in logistic regression

[1] C. W. Groetsch. A Celestial Cubic. Mathematics Magazine, Vol. 74, No. 2 (Apr., 2001), pp. 145–152.