Aatish Bhatia posted something interesting on Twitter: if you define multiplication on Rock, Paper, Scissors to be the winner of a match, the result is commutative but not associative.
Here's a neat thing about the algebra of Rock, Paper, Scissors. If you define 'multiplication' as the game's winner, then it's commutative, i.e.
P x R = R x P = P
S x R = R x S = R
S x P = P x S = SHowever, it isn't associative! e.g., (R x P) x S is not the same as R x (P x S)
— Aatish Bhatia (@aatishb) June 3, 2019
The same is true of the extension Rock, Paper, Scissors, Lizard, Spock
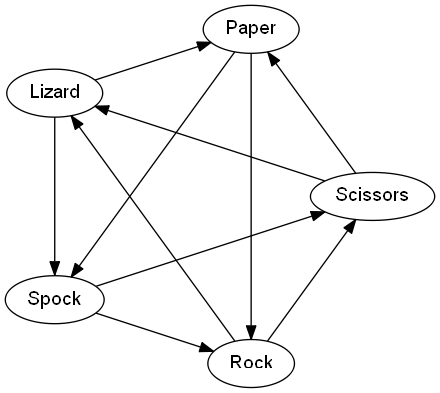 .
.
Related post: Weakening the requirements of a group

It may seems unusual to be commutative but not associative, but
it’s actually somewhat common. I think it’s a big part of the reason floating point arithmetic can be confusing for many people, e.g.