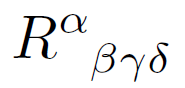
The word “tensor” is shrouded in mystery. The same term is applied to many different things that don’t appear to have much in common with each other.
You might have heard that a tensor is a box of numbers. Just as a matrix is a rectangular collection of numbers, a tensor could be a cube of numbers or even some higher-dimensional set of numbers.
You might also have heard that a tensor is something that has upper and lower indices, such as the Riemann tensor above, things that have arcane manipulation rules such as “Einstein summation.”
Or you might have heard that a tensor is something that changes coordinates like a tensor. A tensor is as a tensor does. Something that behaves the right way under certain changes of variables is a tensor.
And then there’s things that aren’t called tensors, but they have tensor products. These seem simple enough in some cases—you think “I didn’t realize that has a name. So it’s called a tensor product. Good to know.” But then in other cases tensor products seem more elusive. If you look in an advanced algebra book hoping for a simple definition of a tensor product, you might be disappointed and feel like the book is being evasive or even poetic because it describes what a tensor product does rather than what it is. That is, the definition is behavioral rather than constructive.
What do all these different uses of the word “tensor” have to do with each other? Do they have anything to do with the TensorFlow machine learning library that Google released recently? That’s something I’d like to explore over a series of blog posts.

My father’s math skills were pretty good but he admitted to me that after a lot of calculus, matrices, vectors, and physics in College in the late ’50s, he took a class on Tensors and couldn’t understand a bit of it.
I remember when I first studied tensors, in general relativity class, they seemed unmotivated and I couldn’t make much sense of the point of them; I had to drop the class before I got really used to using them. Later I ran across them in their natural development in a book on geodesy and then soon after in a book on crystallography, and after that they made a lot of sense.
I’m really looking forward to hearing your take on teaching tensors!
I think I understand the concept and the importance in physics, but I truggle understanding rigorous definitions like in https://people.math.ethz.ch/~riviere/papers/SkriptDGI+DGII.pdf p.141 – somehow a weird quotient space is used, and it’s not at all intuitive.
One minorthing: I got taught that for tensors, each index should have its own vertical space (to make the decomposition into a tensor product of multiple co-/contravariant rank one tensors unambiguous), so I know the Riemann tensor as $R^\alpha{}_{\beta\gamma\delta}$ instead of $R^\alpha_{\beta\gamma\delta}$. However, I have seen non-tensor quantities like the Christoffel symbols written with “compact” indices.
But that’s just my two cents.
I look forward to this series of posts. Tensors popped up toward the end of my Bachelor’s work as a physics major, and I never really grasped them.
I tried to read Roger Penrose’s /The Road to Reality/, and was able to do as he suggested and more-or-less shrug off most math when it got a bit too intense for me, but eventually ground to a halt realizing I just wouldn’t be able to get through it without grokking tensors first. I’ve tried, and so far haven’t succeeded but have developed the suspicion they’re actually very simple if only one could get past the way they’re explained by the different kinds of specialists who already understand them (there’s a line from Tom Lehrer’s Physical Revue something like, “I understand the subject matter thoroughly, ’tis true, and I can’t see why it isn’t all as obvious to you”). I’ve been thinking if I ever get it figured out I’d try to write a wikibook.
I learned about tensors through studying mechanics. The physical entities stress and strain are prototypical examples of naturally describable tensors built up from dyadic products (forces, deformations, etc). They obey certain natural laws.
When I see Google using the term “tensor”, I think it’s mostly marketing, because really they just seem to me like they are passing multi-dimensional matrices around.
There’s a great video on YouTube called “Tensors/tensor products over-mystified”.
Maybe I’m oversimplifying but isn’t a tensor just a mathematical generalization that can be used to represent arbitrary-dimensional collections, i.e. scalars (zero-dimensional tensor), arrays (one-dimensional tensor), matrices (two-dimensional tensor), etc.?
The components of a tensor are a collection of numbers, but they have more structure. They’re used in a certain way and change a certain way under changes of variables.
Transformation law, shudder. A tensor is “really” something coordinate independent. The “transformation law” is the coordinate expression of coordinate independence. You have to climb a bit to get to where that’s what the view looks like, but it’s worth the effort.
A tensor is really a collection of functions (or sections) rather than a collection of numbers. Indeed, while in most cases matrices we consider [and esp. nearly all those encountered by students] are filled with numbers, this is “almost never” the case for tensors (except for the intertia tensor of a solid, and a few other examples from solid state physics). In particular not for tensors in GR (as the R^a_bcd in the picture). And yes, that’s not the end of the story, because transformation properties are essential. I think one ought to know about vector fields and differential forms to understand tensors as those appearing in GR.