
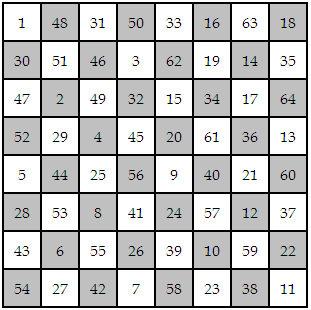
This magic square was created by Leonhard Euler (1707-1783). Each row and each column sum to 260. Each half-row and half-column sum to 130. The square is also a knight’s tour: a knight could visit each square on a chessboard exactly once by following the numbers in sequence.
Here is Python code to verify that the square has the properties listed above.
Update: It seems the attribution to Euler is a persistent error. Euler did publish the first paper on knight’s tours, but the knight’s tour square above was published by William Beverley in 1848. Thanks to George Jelliss for the correction. See the comments below.
Update 2: Notes from George Jelliss on magic king and queen tours.
Update 3: This is technically a semi-magic square: the rows add up to the same magic constant, but the diagonals do not. See Magic square errata.

The tour shown is in fact due to William Beverley and was published in the Philosophical Magazine in 1848. No magic knight tours are known before that date. Leonhard Euler did not compose any magic knight tour. This is an error in the mathematics literature that seems impossible to eradicate!
My “mayhematics” website includes a catalogue of all known magic knight tours on the 8×8 board, and much more on this subject.
I found this magic square in the volume Mathematics From the Life Science Library, edited by David Bergamini, 1963. However, it looks like George Jelliss has done a lot of research in this area and believes this source was wrong to attribute the square to Euler.
Absolutely beautiful, and very unexpected! As a chess enthusiast, I’ve seen plenty of knight tours, but seeing one that is also a magic square is a very pleasant surprise.
Marvellous! How did he (whoever it was) do it?
Regarding the attribution, people love appeals to authority and it is always easier to remember a famous name than one less famous. I think that is one reason for so many incorrect attributions.
Another related reason is hero-worship. People who admire a famous person are quite inclined to believe anything positive about them. I suspect many of the anecdotes about folks like Feyman, Erdos, Einstein and so on are not true in the sense of factual, but they survive because they are true in the sense of conforming to and reinforcing admirers’ images of those folks.
Anyhow, we all know that if it wasn’t Euler, it must have been Gauss, or else Feyman came up with the knight’s tour magic square on the back of a cocktail napkin while trying to pick up a showgirl in Vegas between bongo sets.
Hold on a second — the diagonals don’t add up to 260!
True, the diagonals don’t add to 260. That’s not a feature of this square.
Hmm … OK. I thought that was one of the defining characteristics of a magic square. I can’t recall seeing one where the diagonals didn’t also sum to the same number as the rows and columns.
You might find this article interesting:
http://mathworld.wolfram.com/news/2003-08-06/magictours/
In fact it is impossible to construct an 8×8 knight’s tour with one or both diagonals magic (though together they can add to twice the magic constant, i.e. 520). This was shown in 2003 when a distributed computer project enumerated all 140 possible. That year also Awani Kumar constructed three 12×12 magic knight’s tours that are magic in the diagonals, and I proved that magic knight’s tours on singly even boards (e.g. 6×6 or 10×10) are impossible.
George, that is astonishing! I’ll have to look up your proof. Wow!
It’s certainly the best bit of mathematics I’ve done. In fact it applies to magic rectangle tours too.
The main cause of misattributions in my experience is people jumping to unjustified conclusions, due to only reading the headline, or a loosely worded caption, or something in an unfamiliar language. John V.’s myth about Feynman is a dangerous temptation to fortune!
I heard a person refer to something said by a friend who was relatively well-known. It was certainly the sort of comment that my friend might have enunciated but, in this instance, I was the person who actually came up with the idea.
A strange experience – being subsumed into someone else’s “school”.
Hi,
Do think it would be possible to create a 16×16 magic square using the knights tour on a board of this size?
Thanks
Ravi, it’s been done: http://www.mayhematics.com/t/magic/me.htm
In fact diagonally magic tours on all squares 4n by 4n with n >2 are possible.
The bigger the square the easier they are to construct.
Thanks very much George. Appreciate your sending the link.
Regards
Ravi